In a situation where only one car is travelling along a stretch of highway, densities (in vehicles per kilometre) will by definition be near to zero and the speed at which the car can be driven is determined solely by the geometric design and layout of the road; such a speed is termed free-flow speed as it is in no way hindered by the presence of other vehicles on the highway. As more vehicles use the section of highway, the density of the flow will increase and their speed will decrease from their maximum free-flow value (uf ) as they are increasingly more inhibited by the driving manoeuvres of others. If traffic volumes continue to increase, a point is reached where traffic will be brought to a stop, thus speeds will equal zero (u = 0), with the density at its maximum point as cars are jammed bumper to bumper (termed jam density, kj ).

Thus, the limiting values of the relationship between speed and density are as follows:

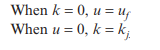
Various attempts have been made to describe the relationship between speed

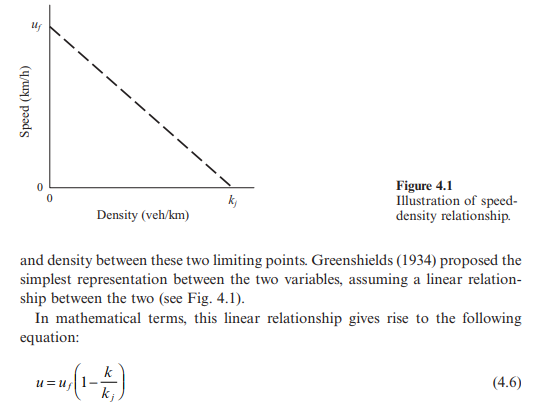
This assumption of linearity allows a direct mathematical linkage to be formed between the speed, flow and density of a stream of traffic.

This linear relationship between speed and density, put forward by Greenshields (1934), leads to a set of mathematical relationships between speed, flow and density as outlined in the next section. The general form of Greenshields’ speed-density relationship can be expressed as:

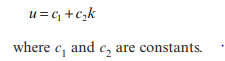
However, certain researchers (Pipes, 1967; Greenberg, 1959) have observed non-linear behaviour at each extreme of the speed-density relationship, i.e. near the free-flow and jam density conditions. Underwood (1961) proposed an exponential relationship of the following form:

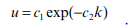
Using this expression, the boundary conditions are:  When density equals zero, the free flow speed equals c1  When speed equals zero, jam density equals infinity. The simple linear relationship between speed and density will be assumed in all the analyses below.

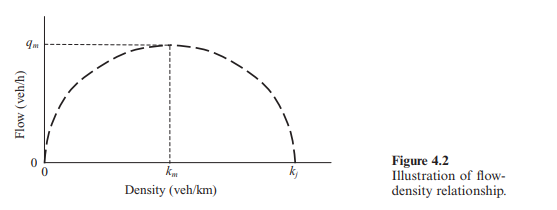
Flow-density relationship

Combining Equations 4.5 and 4.6, the following direct relationship between flow and density is derived:

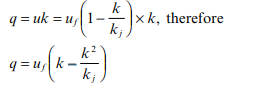4.9

This is a parabolic relationship and is illustrated below in Fig. 4.2.

In order to establish the density at which maximum flow occurs, Equation 4.9 is differentiated and set equal to zero as follows:

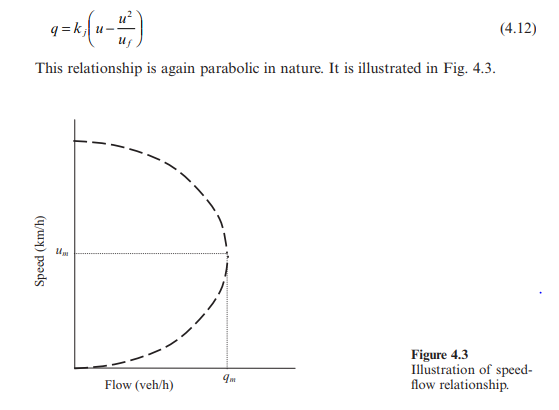
Speed-flow relationship

In order to derive this relationship, Equation 4.6 is rearranged as:

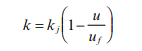
By combining this formula with Equation 4.5, the following relationship is derived: