Hydrostatics

Introduction

Pressure

In fluids we use the term pressure to mean:

The perpendicular force exerted by a fluid per unit area.

This is equivalent to stress in solids, but we shall keep the term pressure. Mathematically, because pressure may vary from place to place, we have:

Pressure Reference Levels

The above diagram shows:

(a) the case when the measured pressure is below atmospheric pressure and so is a negative gauge pressure or a vacuum pressure;

(b)the more usual case when the measured pressure is greater than atmospheric pressure by the gauge pressure.

Pressure in a Fluid

Statics of Definition

We applied the definition of a fluid to the static case previously and determined that there must be no shear forces acting and thus only forces normal to a surface act in a fluid.

For a flat surface at arbitrary angle we have:

And we are not restricted to actual solid-fluid interfaces. We can consider imaginary planes through a fluid:

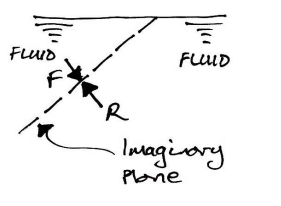
Pascal’s Law

This law states:

 The pressure at a point in a fluid at rest is the same in all directions.

To show this, we will consider a very small wedge of fluid surrounding the point. This wedge is unit thickness into the page:

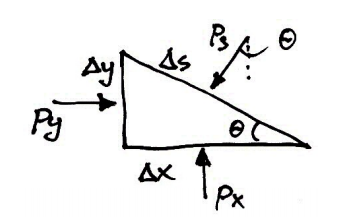
As with all static objects the forces in the x and y directions should balance. Hence:

And so the pressure at a point is the same in any direction. Note that we neglected the weight of the small wedge of fluid because it is infinitesimally small. This is why Pascal’s Law is restricted to the pressure at a point.