Introduction

Hydrostatics involves only a few variables: ρ , g, and h, and so the equations developed are relatively simple and experiment and theory closely agree. The study of fluids in motion is not as simple and accurate. The main difficulty is viscosity.

By neglecting viscosity (an ideal fluid), we do not account for the shear forces which oppose flow. Based on this, reasonably accurate and simple theories can be derived.. Using experimental results, these theories can then be calibrated by using experimental coefficients. They then inherently allow for viscosity.

As we will be dealing with liquids, we will neglect the compressibility of the liquid. This is incompressible flow. This is not a valid assumption for gases.

Classification of Flow Pattern

There are different patterns of fluid flow, usually characterized by time and distance:

·         Time: A flow is steady if the parameters describing it (e.g. flow rate, velocity, pressure, etc.) do not change with time. Otherwise a flow is unsteady.

·         Distance: A flow is uniform if the parameters describing the flow do not change with distance. In non-uniform flow, the parameters change from point to point along the flow.

From these definitions almost all flows will be one of:

Steady uniform flow

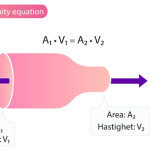
Discharge (i.e. flow rate, or volume per unit time) is constant with time and the cross section of the flow is also constant. Constant flow through a long straight prismatic pipe is an example.

Steady non-uniform flow

The discharge is constant with time, but the cross-section of flow changes. An example is a river with constant discharge, as the cross section of a river changes from point to point.

Unsteady uniform flow

The cross-section is constant but the discharge changes with time resulting in complex flow patterns. A pressure surge in a long straight prismatic pipe is an example.

Unsteady non-uniform flow

Both discharge and cross section vary. A flood wave in a river valley is an example. This is the most complex type of flow.

Visualization

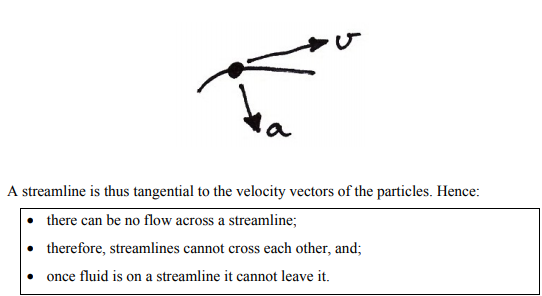
To picture the motion of a fluid, we start by examining the motion of a single fluid ‘particle’ over time, or a collection of particles at one instant. This is the flow path of the particle(s), or a streamline:

At each point, each particle has both velocity and acceleration vectors

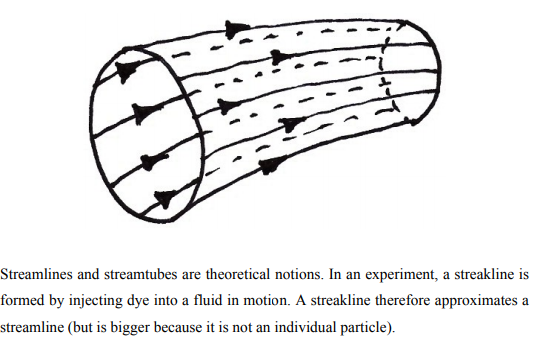
We extend this idea to a collection of paths of fluid particles to create a stream tube:

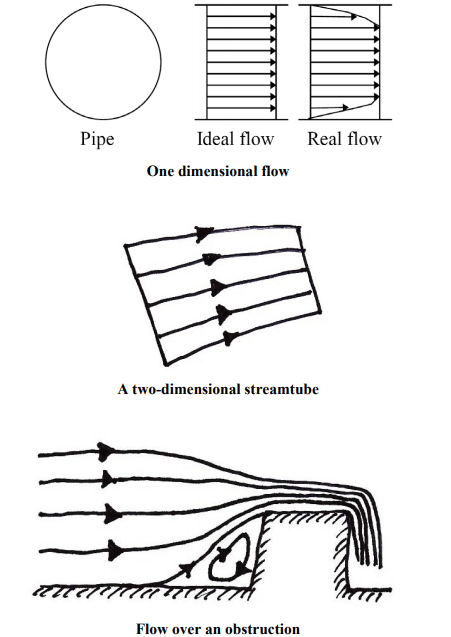
Dimension of Flow

Fluid flow is in general three-dimensional in nature. Parameters of the flow can vary in the x, y and z directions. They can also vary with time. In practice we can reduce problems to one- or two-dimensional flow to simplify. For example: