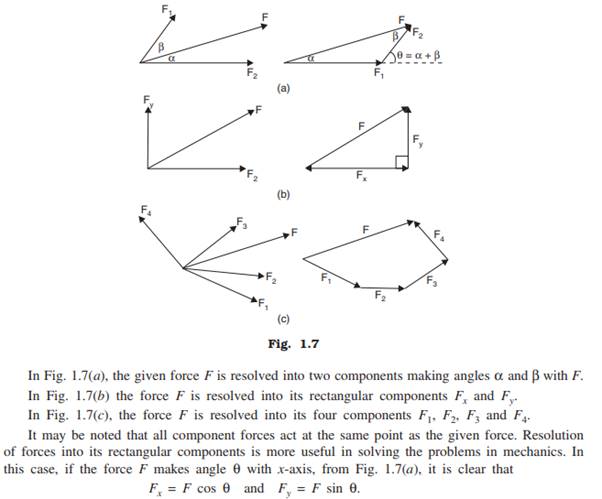
The process of finding a single vector which will have the same effect as a set of vectors acting on a body is known as composition of vectors. The resolution of vectors is exactly the opposite process of composition i.e., it is the process of finding two or more vectors which will have the same effect as that of a vector acting on the body.

Parallelogram Law of Vectors

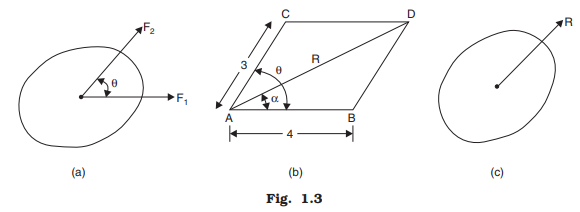
The parallelogram law of vectors enables us to determine the single vector called resultant vector which can replace the two vectors acting at a point with the same effect as that of the two vectors. This law was formulated based on experimental results on a body subjected to two forces. This law can be applied not only to the forces but to any two vectors like velocities, acceleration, momentum etc. Though stevinces employed it in 1586, the credit of presenting it as a law goes to Varignon and Newton (1687). This law states that if two forcer (vectors) acting simultaneously on a body at a point are represented in magnitude and directions by the two adjacent sides of a parallelogram, their resultant is represented in magnitude and direction by the diagonal of the parallelogram which passes thorough the point of intersection of the two sides representing the forces (vectors).

In the Fig. 1.3, the force F1 = 4 units and the force F2 = 3 unit are acting on a body at a point A. To get the resultant of these forces, according to this law, construct the parallelogram ABCD such that AB is equal to 4 units to the linear scale and AC is equal to 3 units. Then according to this law, the diagonal AD represents the resultant in magnitude and direction. Thus the resultant of the forces F1 and F2 is equal to the units corresponding to AD in the direction α to F1.

Triangle Law of Vectors

 Referring to Fig. 1.3 (b), it can be observed that the resultant AD may be obtained by constructing the triangle ABD. Line AB is drawn to represent F1 and BD to represent F2. Then AD should represent the resultant of F1 and F2. Thus we have derived the triangle law of forces from the fundamental law of parallelogram. The Triangle Law of Forces (vectors) may be stated as if two forces (vectors) acting on a body are represented one after another by the sides of a triangle, their resultant is represented by the closing side of the triangle taken from the first point to the last point.

Polygon Law of Forces (Vectors)

If more than two forces (vectors) are acting on a body, two forces (vectors) at a line can be combined by the triangle law, and finally resultant of all forces (vectors) acting on the body may be obtained.

A system of four concurrent forces acting on a body are shown in Fig. 1.4. AB represents F1 and BC represent F2. Hence according to triangle law of forces AC represents the resultant of F1 and F2, say R1.

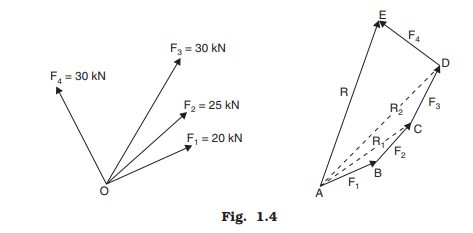
If CD is drawn to represent F3, then from the triangle law of forces AD represents the resultant of R1 and F3. In other words, AD represents the resultant of F1, F2 and F3. Let it be called as R2.

Similarly the logic can be extended to conclude that AE represents the resultant of F1, F2, F3 and F4. The resultant R is represented by the closing line of the polygon ABCDE in the direction from A to E. Thus we have derived the polygon law of the forces (vectors) and it may be stated as if a number of concurrent forces (vectors) acting simultaneously on a body are represented in magnitude and direction by the sides of a polygon, taken in a order, then the resultant is represented in magnitude and direction by the closing side of the polygon, taken from the first point to the last point.

Analytical Method of Composition of Two Vectors

Parallelogram law, triangle law and polygonal law of vectors can be used to find the resultant graphically. This method gives a clear picture of the work being carried out. However the main disadvantage is that it needs drawing aids like pencil, scale, drawing sheets. Hence there is need for analytical method.

Consider the two forces F1 and F2 acting on a particle as shown in Fig 1.5(a). Let the angle between the two forces be θ. If parallelogram ABCD is drawn as shown in Fig. 1.5(b) with AB respresenting F1 and AD representing F2 to some scale, according to parallelogram law of forces AC represents the resultant R. Drop perpendicular CE to AB

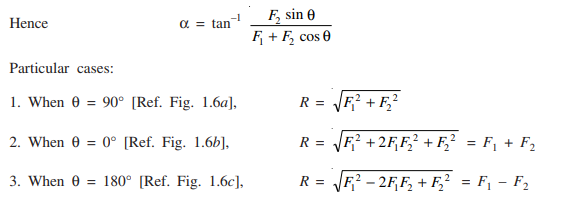
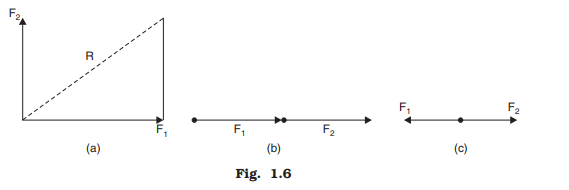
Resolution of Vectors

Since the resolution of vectors is exactly opposite process of composition of vectors, exactly the opposite process of composition can be employed to get the resolved components of a given force.