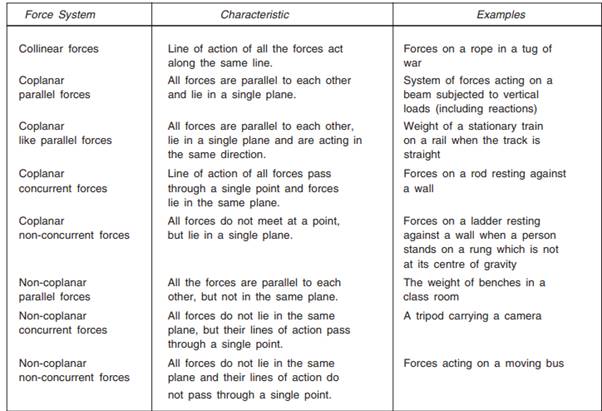
When several forces of different magnitude and direction act upon a body, they constitute a system of forces. If all the forces in a system lie in a single plane, it is called a coplanar force system. If the line of action of all the forces in a system pass through a single point it is called a concurrent force system. In a system of parallel forces all the forces are parallel to each other. If the line of action of all forces lie along a single line then it is called a collinear force system. Various system of forces, their characteristics and examples are given in Table 2.1 below.

Table 2.1 System of Forces

MOMENT OF A FORCE

Moment of a force about a point is the measure of its rotational effect. Moment is defined as the product of the magnitude of the force and the perpendicular distance of the point from the line of action of the force. The point about which the moment is considered is called moment centre and the perpendicular distance of the point from the line of action of the force is called moment arm. Referring to Fig. 2.5, if d1 is the perpendicular distance of point 1 from the line of action of force F, the moment of F about point 1 is given by

VARIGNON’S THEOREM

French mathematician Varignon (1654–1722) gave the following theorem which is also known as principle of moments:

The algebraic sum of the moments of a system of coplanar forces about a moment centre in their plane is equal to the moment of their resultant force about the same moment centre.

Proof: Referring to Fig. 2.6 let R be the resultant of forces F1 and F2 and B the moment centre. Let d, d1 and d2 be the moment arms of the forces, R, F1 and F2, respectively from the moment centre B. Then in this case, we have to prove that:

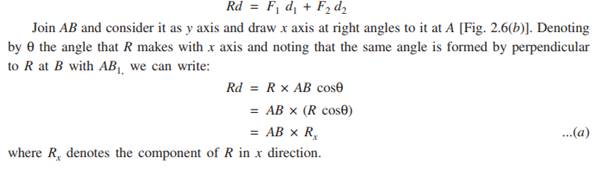
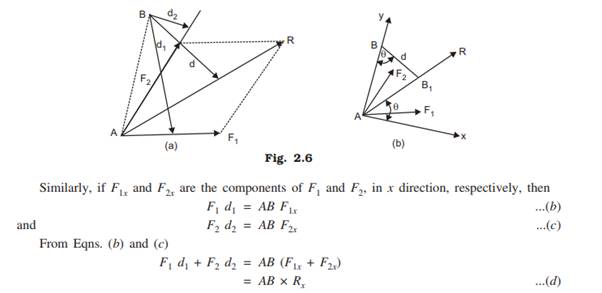
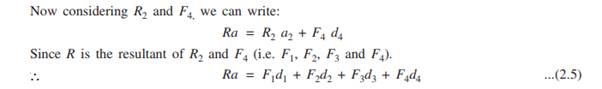
Thus, the moment of the resultant of a number of forces about a moment centre is equal to the sum of the moments of its component forces about the same moment centre.