General Approach

The composition of concurrent forces by graphical method and the analytical method of composition of two force system has been discussed. In this article composition of concurrent coplanar forces is explained by a general analytic method.

Analytical method consists in finding the components of given forces in two mutually perpendicular directions and then combining them to get the resultant. Finding the component of a force is called resolution of forces and is exactly the opposite to the process of composition of forces. Finding the components of forces in two mutually perpendicularly directions is preferable. The following points associated with the analytical method of finding rectangular components may be noted:

(i) Imagine that the arrow drawn to show force represents it to some scale

(ii) Travel from tail to head of the arrow in the directions of coordinates

(iii) The direction of the travel gives the direction of component forces

(iv) From the triangle law of forces, the magnitude of the components can be calculated.

After finding the components of all the forces in the system in the two mutually perpendicular directions, the component in each direction are algebraically added to get the two components. These two components, which are mutually perpendicular, are combined to get the resultant.

Let F1, F2, F3 and F4 shown in Fig. 2.12(a) be the system of four forces the resultant of which is required.

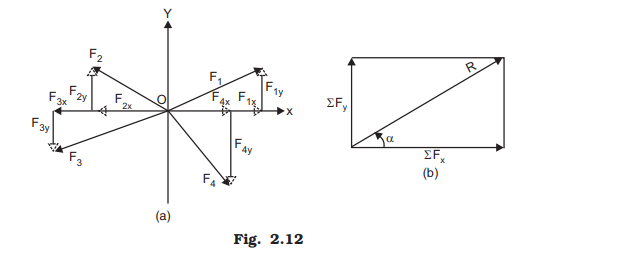
The procedure to get the resultant is given below:

Step 1: Find the components of all the forces in X and Y directions. Thus, F1x, F2x, F3x, F4x, F1y, F2y, F3y, and F4y, are obtained.

Step 2: Find the algebraic sum of the component forces in X and Y directions

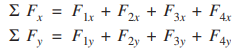
(Note: In the above case F2x, F3x, F3Y and F4Y have negative values.)

Step 3: Now the system of forces is equal to two mutually perpendicular forces, namely, ΣFx and ΣFy as shown in Fig. 2.12(b). Since these two forces are perpendicular, the parallelogram of forces becomes a rectangle. Hence the resultant R is given by