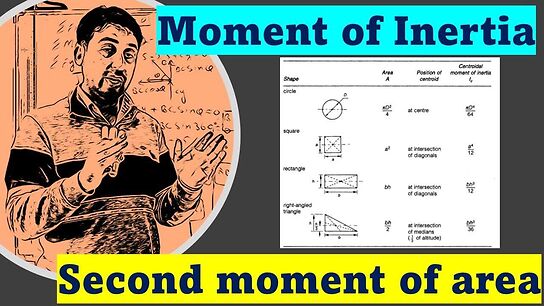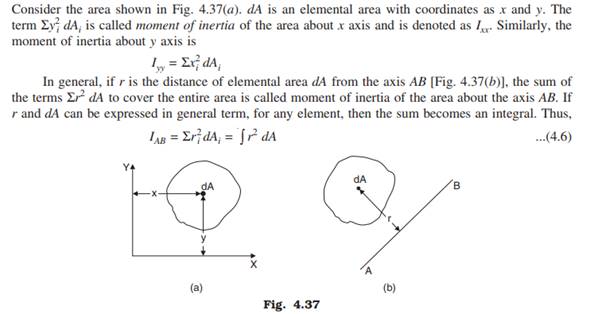
The term rdA may be called as moment of area, similar to moment of a force, and hence r 2 dA may be called as moment of area or the second moment of area. Thus, the moment of inertia of area is nothing but second moment of area. In fact, the term ‘second moment of area’ appears to correctly signify the meaning of the expression Σr ^2 dA. The term ‘moment of inertia’ is rather a misnomer. However, the term moment of inertia has come to stay for long time and hence it will be used in this book also.
Though moment of inertia of plane area is a purely mathematical term, it is one of the important properties of areas. The strength of members subject to bending depends on the moment of inertia of its cross-sectional area. Students will find this property of area very useful when they study subjects like strength of materials, structural design and machine design.
The moment of inertia is a fourth dimensional term since it is a term obtained by multiplying area by the square of the distance. Hence, in SI units, if metre (m) is the unit for linear measurements

Polar Moment of Inertia

Radius of Gyration
Radius of gyration is a mathematical term defined by the relation

The relation between radius of gyration and moment of inertia can be put in the form:

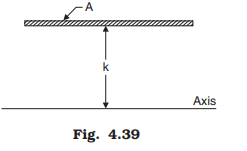
From the above relation a geometric meaning can be assigned to the term ‘radius of gyration.’ We can consider k as the distance at which the complete area is squeezed and kept as a strip of negligible width (Fig. 4.39) such that there is no change in the moment of inertia.