Let F1, F2 and F3 [Fig. 2.18(a)] constitute a system of forces acting on a body. Each force can be replaced by a force of the same magnitude and acting in the same direction at point O and a moment about O. Thus, the given system in Fig. 2.18(a) is equal to the system shown in Fig. 2.18(b) where ΣMO is the algebraic sum of the moments of the given forces about O.

At O, the concurrent force F1, F2 and F3 can be combined as usual to get the resultant force R. Now the resultant of the given system is equal to force R at O and a moment ΣMO as shown in Fig. 2.18(c).

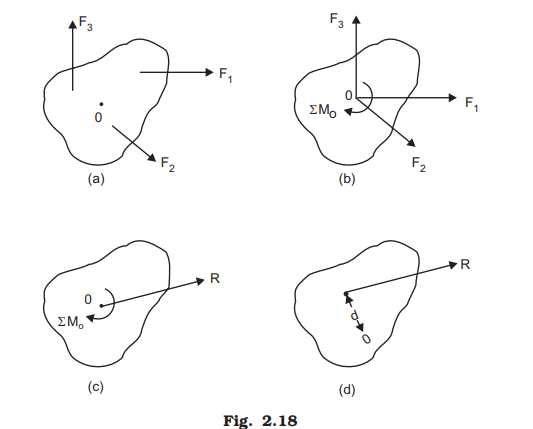
The force R and moment ΣMO shown in Fig. 2.18(c) can be replaced by a single force R acting at a distance d from O such that the moment produced by this force R is equal to ΣMO [Ref. 2.18(d)].

Thus, we get a single force R acting at a distance d from the point O which gives the same effect as the constituent forces of the systems. Thus, the resultant of the given forces may be reduced to a single force.

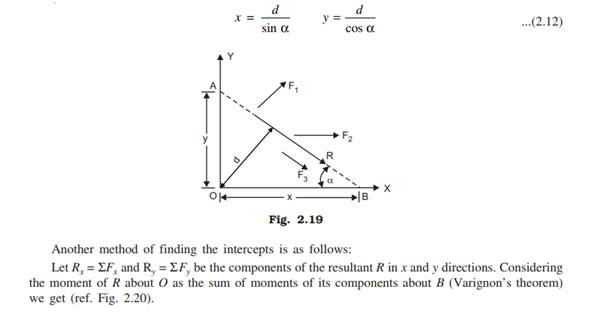
x AND y INTERCEPTS OF RESULTANT

In some situations we may be interested in finding only the distance of R along x or y axis, that is x and y intercepts.

Let d be the distance of the resultant from O and α be its inclination to x axis (Fig. 2.19). Then the intercepts are given by: