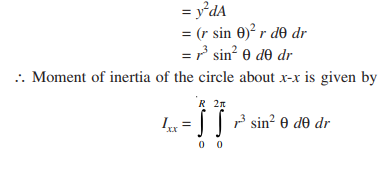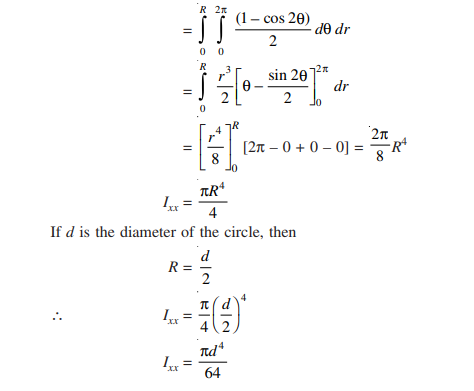For simple figures, moment of inertia can be obtained by writing the general expression for an element and then carrying out integration so as to cover the entire area. This procedure is illustrated with the following three cases:

(1) Moment of inertia of a rectangle about the centroidal axis

(2) Moment of inertia of a triangle about the base

(3) Moment of inertia of a circle about a diametral axis

(1) Moment of Inertia of a Rectangle about the Centroidal Axis:

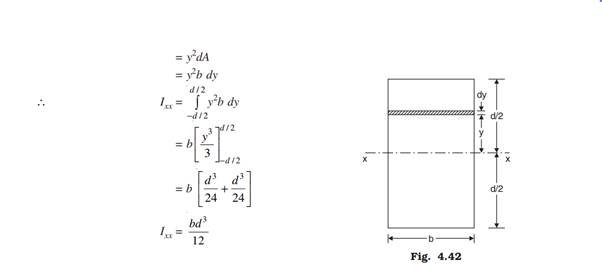
Consider a rectangle of width b and depth d (Fig. 4.42). Moment of inertia about the centroidal axis x-x parallel to the short side is required.

Consider an elemental strip of width dy at a distance y from the axis. Moment of inertia of the elemental strip about the centroidal axis xx is:

(2) Moment of Inertia of a Triangle about its Base:

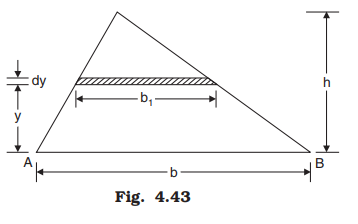
Moment of inertia of a triangle with base width b and height h is to be determined about the base AB (Fig. 4.43).

Consider an elemental strip at a distance y from the base AB. Let dy be the thickness of the strip and dA its area. Width of this strip is given by:

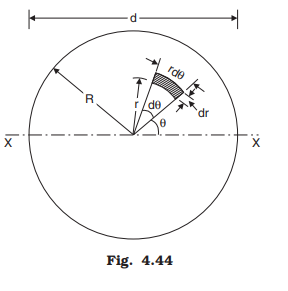
(3) Moment of Inertia of a Circle about its Diametral Axis:

Moment of inertia of a circle of radius R is required about it’s diametral axis as shown in Fig. 4.44 Consider an element of sides rdθ and dr as shown in the figure. It’s moment of inertia about the diametral axis x-x: