In this chapter general meaning of stress is explained. Expressions for stresses and strains is derived with the following assumptions:
1. For the range of forces applied the material is elastic i.e. it can regain its original shape and size, if the applied force is removed.
2. Material is homogeneous i.e. every particle of the material possesses identical mechanical properties.
3. Material is isotropic i.e. the material possesses identical mechanical property at any point in any direction.
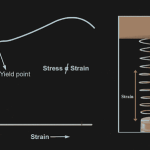
Presenting the typical stress-strain curve for a typical steel, the commonly referred terms like limits of elasticity and proportionality, yield points, ultimate strength and strain hardening are explained.
Linear elastic theory is developed to analyse different types of members subject to axial, shear, thermal and hoop stresses.
MEANING OF STRESS
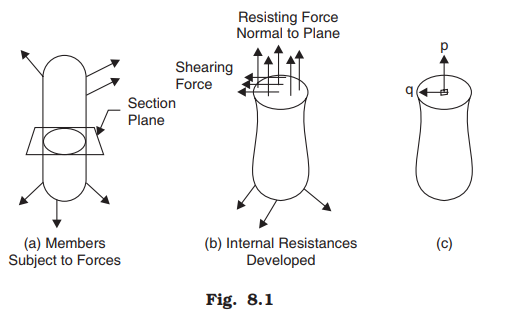
When a member is subjected to loads it develops resisting forces. To find the resisting forces developed a section plane may be passed through the member and equilibrium of any one part may be considered. Each part is in equilibrium under the action of applied forces and internal resisting forces. The resisting forces may be conveniently split into normal and parallel to the section plane. The resisting force parallel to the plane is called shearing resistance. The intensity of resisting force normal to the sectional plane is called intensity of Normal Stress.

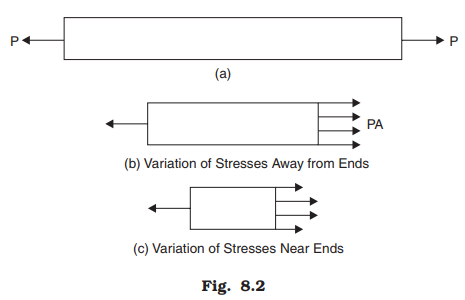
At any cross-section, stress developed may or may not be uniform. In a bar of uniform cross section subject to axial concentrated loads as shown in Fig. 8.2a, the stress is uniform at a section away from the applied loads (Fig. 8.2b); but there is variation of stress at the section near the applied loads (Fig. 8.2c).
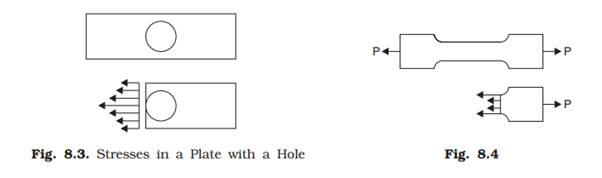
Similarly stress near the hole or at fillets will not be uniform as shown in Figs. 8.3 and 8.4. It is very common that at some points in such regions maximum stress will be as high as 2 to 4 times the average stresses.
STRAIN
No material is perfectly rigid. Under the action of forces a rubber undergoes changes in shape and size. This phenomenon is very well known to all since in case of rubber, even for small forces deformations are quite large. Actually all materials including steel, cast iron, brass, concrete, etc. undergo similar deformation when loaded. But the deformations are very small and hence we cannot see them with naked eye. There are instruments like extensometer, electric strain gauges which can measure extension of magnitude 1/100th, 1/1000th of a millimetre. There are machines like universal testing machines in which bars of different materials can be subjected to accurately known forces of magnitude as high as 1000 kN. The studies have shown that the bars extend under tensile force and shorten under compressive forces as shown in Fig. 8.7. The change in length per unit length is known as linear strain. Thus,
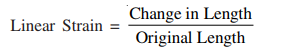
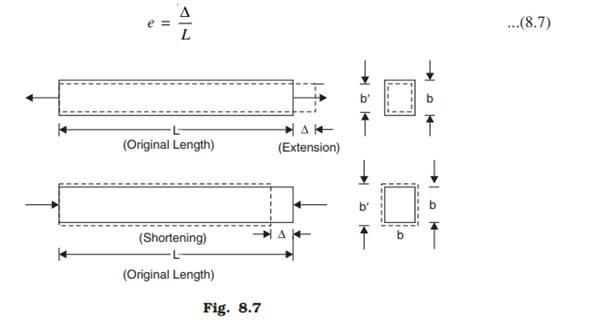
When changes in longitudinal direction is taking place changes in lateral direction also take place. The nature of these changes in lateral direction are exactly opposite to that of changes in longitudinal direction i.e., if extension is taking place in longitudinal direction, the shortening of lateral dimension takes place and if shortening is taking place in longitudinal direction extension takes place in lateral directions (See Fig. 8.7). The lateral strain may be defined as changes in the lateral dimension per unit lateral dimension. Thus,