As the name implies, rigid pavements are rigid i.e, they do not flex much under loading like flexible pavements. They are constructed using cement concrete. In this case, the load carrying capacity is mainly due to the rigidity ad high modulus of elasticity of the slab (slab action). H. M. Westergaard is considered the pioneer in providing the rational treatment of the rigid pavement analysis.
Modulus of sub-grade reaction
Westergaard considered the rigid pavement slab as a thin elastic plate resting on soil sub-grade, which is assumed as a dense liquid. The upward reaction is assumed to be proportional to the deflection. Base on this assumption, Westergaard defined a modulus of sub-grade reaction ![]() in kg/cm
in kg/cm![]() given by
given by ![]() where
where ![]() is the displacement level taken as 0.125 cm and
is the displacement level taken as 0.125 cm and ![]() is the pressure sustained by the rigid plate of 75 cm diameter at a deflection of 0.125 cm.
is the pressure sustained by the rigid plate of 75 cm diameter at a deflection of 0.125 cm.
Relative stiffness of slab to sub-grade
A certain degree of resistance to slab deflection is offered by the sub-grade. The sub-grade deformation is same as the slab deflection. Hence the slab deflection is direct measurement of the magnitude of the sub-grade pressure. This pressure deformation characteristics of rigid pavement lead Westergaard to the define the term radius of relative stiffness ![]() in cm is given by the equation .
in cm is given by the equation .
where E is the modulus of elasticity of cement concrete in kg/cm![]() (3.0
(3.0![]() 10
10![]() ),
), ![]() is the Poisson’s ratio of concrete (0.15),
is the Poisson’s ratio of concrete (0.15), ![]() is the slab thickness in cm and
is the slab thickness in cm and ![]() is the modulus of sub-grade reaction.
is the modulus of sub-grade reaction.
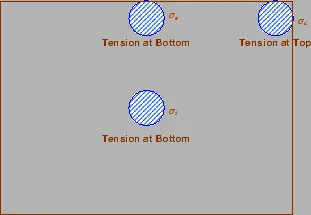
Critical load positions
Since the pavement slab has finite length and width, either the character or the intensity of maximum stress induced by the application of a given traffic load is dependent on the location of the load on the pavement surface. There are three typical locations namely the interior, edge and corner, where differing conditions of slab continuity exist. These locations are termed as critical load positions.
Equivalent radius of resisting section
When the interior point is loaded, only a small area of the pavement is resisting the bending moment of the plate. Westergaard’s gives a relation for equivalent radius of the resisting section in cm in the equation .
where ![]() is the radius of the wheel load distribution in cm and
is the radius of the wheel load distribution in cm and ![]() is the slab thickness in cm.
is the slab thickness in cm.
Wheel load stresses – Westergaard’s stress equation
The cement concrete slab is assumed to be homogeneous and to have uniform elastic properties with vertical sub-grade reaction being proportional to the deflection. Westergaard developed relationships for the stress at interior, edge and corner regions, denoted as ![]() in kg/cm
in kg/cm![]() respectively and given by the equation –.
respectively and given by the equation –.
where ![]() is the slab thickness in cm,
is the slab thickness in cm, ![]() is the wheel load in kg,
is the wheel load in kg, ![]() is the radius of the wheel load distribution in cm,
is the radius of the wheel load distribution in cm, ![]() the radius of the relative stiffness in cm and
the radius of the relative stiffness in cm and ![]() is the radius of the resisting section in cm
is the radius of the resisting section in cm
Temperature stresses
Temperature stresses are developed in cement concrete pavement due to variation in slab temperature. This is caused by
(i) daily variation resulting in a temperature gradient across the thickness of the slab and
(ii) seasonal variation resulting in overall change in the slab temperature. The former results in warping stresses and the later in frictional stresses.
Warping stress
The warping stress at the interior, edge and corner regions, denoted as ![]() in kg/cm
in kg/cm![]() respectively and given by the equation –.
respectively and given by the equation –.
| (7) |
where ![]() is the modulus of elasticity of concrete in kg/cm
is the modulus of elasticity of concrete in kg/cm![]() (3
(3![]() 10
10![]() ),
), ![]() is the thermal coefficient of concrete per
is the thermal coefficient of concrete per ![]() C (1
C (1![]() 10
10![]() )
) ![]() is the temperature difference between the top and bottom of the slab,
is the temperature difference between the top and bottom of the slab, ![]() and
and ![]() are the coefficient based on
are the coefficient based on ![]() in the desired direction and
in the desired direction and ![]() right angle to the desired direction,
right angle to the desired direction, ![]() is the Poisson’s ration (0.15),
is the Poisson’s ration (0.15), ![]() is the radius of the contact area and
is the radius of the contact area and ![]() is the radius of the relative stiffness.
is the radius of the relative stiffness.
Frictional stresses
The frictional stress ![]() in kg/cm
in kg/cm![]() is given by the equation
is given by the equation
| (9) |
where ![]() is the unit weight of concrete in kg/cm
is the unit weight of concrete in kg/cm![]() (2400),
(2400), ![]() is the coefficient of sub grade friction (1.5) and
is the coefficient of sub grade friction (1.5) and ![]() is the length of the slab in meters.
is the length of the slab in meters.
Combination of stresses
The cumulative effect of the different stress give rise to the following thee critical cases
- Summer, mid-day: The critical stress is for edge region given by
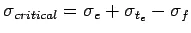
- Winter, mid-day: The critical combination of stress is for the edge region given by
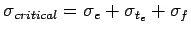
- Mid-nights: The critical combination of stress is for the corner region given by
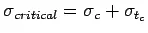
Design of joints
Expansion joints
The purpose of the expansion joint is to allow the expansion of the pavement due to rise in temperature with respect to construction temperature. The design consideration are:
- Provided along the longitudinal direction,
- design involves finding the joint spacing for a given expansion joint thickness (say 2.5 cm specified by IRC) subjected to some maximum spacing (say 140 as per IRC)
Contraction joints
The purpose of the contraction joint is to allow the contraction of the slab due to fall in slab temperature below the construction temperature. The design considerations are:
- The movement is restricted by the sub-grade friction
- Design involves the length of the slab given by:
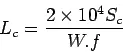 | (10) |
- where,
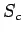 is the allowable stress in tension in cement concrete and is taken as 0.8 kg/cm
is the allowable stress in tension in cement concrete and is taken as 0.8 kg/cm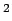 ,
, 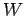 is the unit weight of the concrete which can be taken as 2400 kg/cm
is the unit weight of the concrete which can be taken as 2400 kg/cm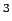 and
and 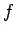 is the coefficient of sub-grade friction which can be taken as 1.5.
is the coefficient of sub-grade friction which can be taken as 1.5. - Steel reinforcements can be use, however with a maximum spacing of 4.5 m as per IRC.
Dowel bars
The purpose of the dowel bar is to effectively transfer the load between two concrete slabs and to keep the two slabs in same height. The dowel bars are provided in the direction of the traffic (longitudinal). The design considerations are:
- Mild steel rounded bars,
- bonded on one side and free on other side
Bradbury’s analysis
Bradbury’s analysis gives load transfer capacity of single dowel bar in shear, bending and bearing as follows:
where, ![]() is the load transfer capacity of a single dowel bar in shear
is the load transfer capacity of a single dowel bar in shear ![]() , bending
, bending ![]() and bearing
and bearing ![]() ,
, ![]() is the diameter of the bar in cm,
is the diameter of the bar in cm, ![]() is the length of the embedment of dowel bar in cm,
is the length of the embedment of dowel bar in cm, ![]() is the joint width in cm,
is the joint width in cm, ![]() are the permissible stress in shear, bending and bearing for the dowel bar in kg/cm
are the permissible stress in shear, bending and bearing for the dowel bar in kg/cm![]() .
.
Design procedure
Step Find the length of the dowel bar embedded in slab ![]() by equating Eq. =Eq. , i.e.
by equating Eq. =Eq. , i.e.
Step Find the load transfer capacities ![]() ,
, ![]() , and
, and ![]() of single dowel bar with the
of single dowel bar with the ![]()
Step Assume load capacity of dowel bar is 40 percent wheel load, find the load capacity factor f as
Step Spacing of the dowel bars.
- Effective distance upto which effective load transfer take place is given by
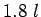 , where
, where  is the radius of relative stiffness.
is the radius of relative stiffness. - Assume a linear variation of capacity factor of 1.0 under load to 0 at
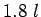 .
. - Assume a dowel spacing and find the capacity factor of the above spacing.
- Actual capacity factor should be greater than the required capacity factor.
- If not, do one more iteration with new spacing.
Example
Design size and spacing of dowel bars at an expansion joint of concrete pavement of thickness 25 cm. Given the radius of relative stiffness of 80 cm. design wheel load 5000 kg. Load capacity of the dowel system is 40 percent of design wheel load. Joint width is 2.0 cm and the permissible stress in shear, bending and bearing stress in dowel bars are 1000,1400 and 100 ![]() respectively.
respectively.
Solution:
Given, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() ; and assume
; and assume ![]() diameter.
diameter.
Step-1: length of the dowel bar ![]()
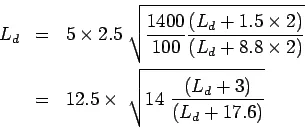
Solve for ![]() by trial and error:
by trial and error:
put ![]() put
put ![]() put
put ![]() Minimum length of the dowel bar is
Minimum length of the dowel bar is ![]() , So, provide
, So, provide ![]() long and
long and ![]() . Therefore
. Therefore ![]() .
.
Step 2: Find the load transfer capacity of single dowel bar
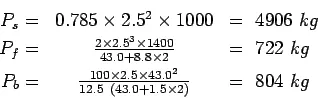
Therefore, the required load transfer capacity
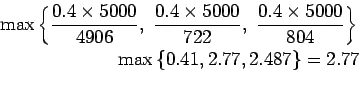
Step-3 : Find the required spacing: Effective distance of load transfer ![]() . Assuming
. Assuming ![]() spacing,
spacing,
Actual capacity is
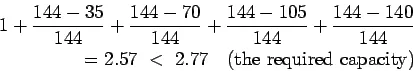
Therefore assume ![]() spacing and now the actual capacity is
spacing and now the actual capacity is
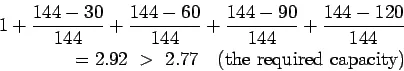
Therefore provide ![]() mild steel dowel bars of length
mild steel dowel bars of length ![]() center to center.
center to center.
Tie bars
In contrast to dowel bars, tie bars are not load transfer devices, but serve as a means to tie two slabs. Hence tie bars must be deformed or hooked and must be firmly anchored into the concrete to function properly. They are smaller than dowel bars and placed at large intervals. They are provided across longitudinal joints.
Step Diameter and spacing: The diameter and the spacing is first found out by equating the total sub-grade friction tot he total tensile stress for a unit length (one meter). Hence the area of steel per one meter in ![]() is given by:
is given by:
where, ![]() is the width of the pavement panel in
is the width of the pavement panel in ![]() ,
, ![]() is the depth of the pavement in
is the depth of the pavement in ![]() ,
, ![]() is the unit weight of the concrete (assume
is the unit weight of the concrete (assume ![]() ),
), ![]() is the coefficient of friction (assume
is the coefficient of friction (assume ![]() ), and
), and ![]() is the allowable working tensile stress in steel (assume
is the allowable working tensile stress in steel (assume ![]() ). Assume
). Assume ![]() to
to ![]() bars for the design.
bars for the design.
Step Length of the tie bar: Length of the tie bar is twice the length needed to develop bond stress equal to the working tensile stress and is given by:
where, ![]() is the diameter of the bar,
is the diameter of the bar, ![]() is the allowable tensile stress in
is the allowable tensile stress in ![]() , and
, and ![]() is the allowable bond stress and can be assumed for plain and deformed bars respectively as
is the allowable bond stress and can be assumed for plain and deformed bars respectively as ![]() and
and ![]() .
.
Example
A cement concrete pavement of thickness 18 cm, has two lanes of 7.2 m with a joint. Design the tie bars. (Solution:) Given h=18 cm, b=7.2/2=3.6m, ![]()
![]()
![]()
![]() . Step 1: diameter and spacing: Get
. Step 1: diameter and spacing: Get ![]() from
from
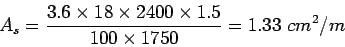
Assume ![]() . Therefore spacing is
. Therefore spacing is ![]() , say
, say ![]() Step 2: Length of the bar: Get
Step 2: Length of the bar: Get ![]() from
from
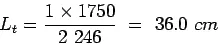
[Ans] Use ![]() tie bars of length of
tie bars of length of ![]()
Summary
Design of rigid pavements is based on Westergaard’s analysis, where modulus of subgrade reaction, radius of relative stiffness, radius of wheel load distribution are used. For critical design, a combination of load stress, frictional stress and warping stress is considered. Different types of joints are required like expansion and contraction joints. Their design is also dealt with.

![Description: \begin{displaymath}
l = \sqrt[4]{\frac{Eh^3}{12K(1-\mu^2)}}
\end{displaymath}](https://appassets.softecksblog.in/civil_engineering/assets/pavement/11_files/image008.webp)
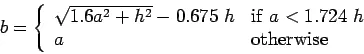
![Description: \begin{displaymath}
\sigma_i=\frac{0.316 P}{h^2}\left[4 \log_{10}\left(\frac{l}{b}\right)+1.069\right]
\end{displaymath}](https://appassets.softecksblog.in/civil_engineering/assets/pavement/11_files/image018.webp)
![Description: \begin{displaymath}
\sigma_e=\frac{0.572 P}{h^2}\left[4 \log_{10}\left(\frac{l}{b}\right)+0.359\right]
\end{displaymath}](https://appassets.softecksblog.in/civil_engineering/assets/pavement/11_files/image019.webp)
![Description: \begin{displaymath}
\sigma_c=\frac{3 P}{h^2}\left[1-\left(\frac{a\sqrt{2}}{l}\right)^{0.6}\right]
\end{displaymath}](https://appassets.softecksblog.in/civil_engineering/assets/pavement/11_files/image020.webp)
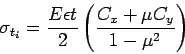
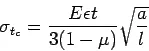
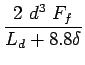
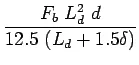
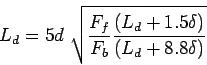
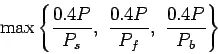
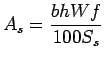
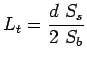


Comments are closed