Porosity

Soils usually consist of particles, water and air. In order to describe a soil various parameters are used to describe the distribution of these three components, and their relative contribution to the volume of a soil. These are also useful to determine other parameters, such as the weight of the soil. They are defined in this chapter.

An important basic parameter is the porosity n, defined as the ratio of the volume of the pore space and the total volume of the soil,

For most soils the porosity is a number between 0.30 and 0.45 (or, as it is usually expressed as a percentage, between 30 % and 45 %). When the porosity is small the soil is called densely packed, when the porosity is large it is loosely packed .

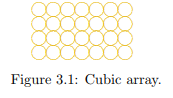
It may be interesting to calculate the porosities for two particular cases. The first case is a very loose packing of spherical particles, in which the contacts between the spheres occur in three mutually orthogonal directions only. This is called a cubic array of particles, see Figure 3.1. If the diameter of the spheres is D, each sphere occupies a volume πD3/6 in space. The ratio of the volume of the solids to the total volume then is Vp/Vt = π/6 = 0.5236, and the porosity of this assembly thus is n = 0.4764. This is the loosest packing of spherical particles that seems possible. Of course, it is not stable: any small disturbance will make the assembly collapse.

A very dense packing of spheres can be constructed by starting form layers in which the spheres form a pattern of equilateral triangle, see Figure 3.2. The packing is constructed by packing such layers such that the spheres of the next layer just fit in the hollow space between three spheres of the previous layer. The axial lines from a sphere with the three spheres that support it from below form an regular tetrahedron, having sides of magnitude D. The height of each tetrahedron is D p 2/3. Each sphere of the assembly, with its neighbouring part of the voids, occupies a volume in space of magnitude D × (D p 3/4) × (D p 2/3) = D3p 1/2. Because the volume of the sphere itself is πD3/6 is, the porosity of this assembly is n = 1 − π/√ 18 = 0.2595. This seems to be the most dense packing of a set of spherical particles.

Although soils never consist of spherical particles, and the values calculated above have no real meaning for actual soils, they may give a certain indication of what the porosity of real soils may be. It can thus be expected that the porosity n of a granular material may have a value somewhere in the range from 0.25 to 0.45. Practical experience confirms this statement.

The amount of pores can also be expressed in the void ratio e, defined as the ratio of the volume of the pores to the volume of the solids,

In many countries this quantity is prefered to the porosity, because it expresses the pore volume with respect to a fixed volume (the volume of the solids). Because the total volume of the soil is the sum of the volume of the pores and the volume of the solids, Vt = Vp + Vs, the porosity and the void ratio can easily be related,

The porosity can not be smaller than 0, and can not be greater than 1. The void ratio can be greater than 1. The void ratio is also used in combination with the relative density. This quantity is defined as

Here emax is the maximum possible void ratio, and emin the minimum possible value. These values may be determined in the laboratory. The densest packing of the soil can be obtained by strong vibration of a s ample, which then gives emin. The loosest packing can be achieved by carefully pouring the soil into a container, or by letting the material subside under water, avoiding all disturbances, which gives emax. The accuracy of the determination of these two values is not very large. After some more vibration the sample may become even denser, and the slightest disturbance may influence a loose packing. It follows from eq. (3.4) that the relative density varies between 0 and 1. A small value, say RD < 0.5, means that the soil can easily be densified. Such a densification can occur in the field rather unexpectedly, for instance in case of a sudden shock (an earthquake), with dire consequences.

Of course, the relative density can also be expressed in terms of the porosity, using eqs. (3.3), but this leads to an inconvenient formula, and therefore this is unusual.

Degree of saturation

The pores of a soil may contain water and air. To describe the ratio of these two the degree of saturation S is introduced as

Here Vw is the volume of the water, and Vp is the total volume of the pore space. The volume of air (or any other gas) per unit pore space then is 1 − S. If S = 1 the soil is completely saturated, if S = 0 the soil is perfectly dry.