For the description of the density and the volumetric weight of a soil, the densities of the various components are needed. The density of a substance is the mass per unit volume of that substance. For water this is denoted by ρw, and its value is about 1000 kg/m3 . Small deviations from this value may occur due to temperature differences or variations in salt content. In soil mechanics these are often of minor importance, and it is often considered accurate enough to assume that

For the analysis of soil mechanics problems the density of air can usually be disregarded.

The density of the solid particles depends upon the actual composition of the solid material. In many cases, especially for quartz sands, its value is about

This value can be determined by carefully dropping a certain mass of particles (say Wp) in a container partially filled with water, see Figure 3.3. The precise volume of the particles can be measured by observing the rise of the water table in the glass. This is particularly easy when using a graduated measuring glass. The rising of the water table indicates the volume of the particles, Vp. Their mass Wp can be measured most easily

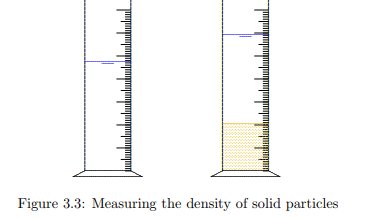
by measuring the weight of the glass before and after dropping the particles in it. The density of the particle material then follows immediately from its definition,

For sand the value of ρp usually is about 2650 kg/m3.

The principle of this simple test, in which the volume of a body having a very irregular shape (a number of sand particles) is measured is due to Archimedes. He had been asked to check the composition of a golden crown, of which it was suspected that it contained silver (which is cheaper). He realized that this could be achieved by comparing the density of the crown with the density of a piece of pure gold, but then he had to determine the precise volume of the crown. The legend has it that when stepping into his bath he discovered that the volume of a body submerged in water equals the volume of water above the original water table. While shouting ”Eureka!” he ran into the street, according to the legend.

Volumetric weight

using eq. (3.10). Unfortunately, this procedure is not very accurate for soils that are almost completely saturated, because a small error in the measurements may cause that one obtains, for example, S = 0.97 rather than the true value S = 0.99. In itself this is rather accurate, but the error in the air volume is then 300 %. In some cases, this may lead to large errors, for instance when the compressibility of the water-air-mixture in the pores must be determined.

Water content

The water content is another useful parameter, especially for clays. It has been used in the previous chapter. By definition the water content w is the ratio of the weight (or mass) of the water and the solids,