Stresses

As in other materials, stresses may act in soils as a result of an external load and the volumetric weight of the material itself. Soils, however, have a number of properties that distinguish it from other materials. Firstly, a special property is that soils can only transfer compressive normal stresses, and no tensile stresses. Secondly, shear stresses can only be transmitted if they are relatively small, compared to the normal stresses. Furthermore,

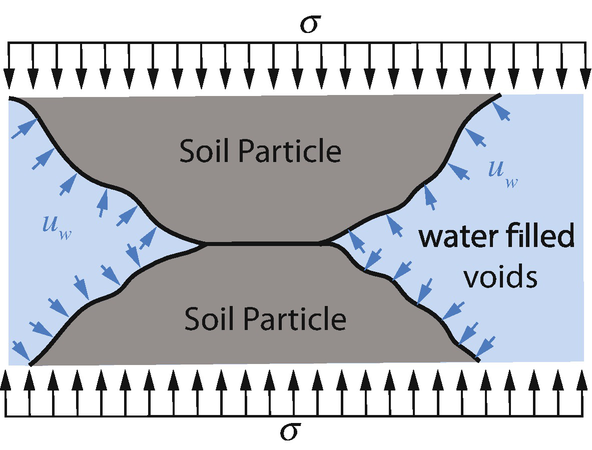
it is characteristic of soils that part of the stresses is transferred by the water in the pores. This will be considered in detail in this chapter.

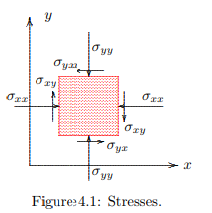
Because the normal stresses in soils usually are compressive stresses only, it is standard practice to use a sign convention for the stresses that is just opposite to the sign convention of classical continuum mechanics, namely such that compressive stresses are considered positive, and tensile stresses are negative. De stress tensor will be denoted by σ. The sign convention for the stress components is illustrated in Figure 4.1. Its definition is that a stress component when it acts in a positive coordinate direction on a plane with its outward normal in a negative coordinate direction, or when it acts in negative direction on a plane in positive direction. This means that the sign of all stress components is just opposite to the sign that they would have in most books on continuum mechanics or in applied mechanics.

It is assumed that in indicating a stress component σij the first index denotes the plane on which the stress is acting, and the second index denotes the direction of the stress itself. This means, for instance, that the stress component σxy indicates that the force y-direction, acting upon a plane having its normal in the x-direction is Fy = −σxyAx, where Ax denotes the area of the plane surface. The minus sign is needed because of the sign convention of soil mechanics, assuming that the sign convention for forces is the same as in mechanics in general.

Pore pressures

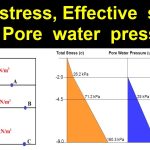
Soil is a porous material, consisting of particles that together constitute the grain skeleton. In the pores of the grain skeleton a fluid may be present: usually water. The pore structure of all normal soils is such that the pores are mutually connected. The water fills a space of very complex form, but it constitutes a single continuous body. In this water body a pressure may be transmitted, and the water may also flow thorugh the pores. The pressure in the pore water is denoted as the pore pressure. In a fluid at rest no shear stresses can be transmitted. This means that the pressure is the same in all directions. This can be proved by considering the equilibrium conditions of a small triangular element, see Figure 4.2, bounded by a vertical plane, a horizontal plane and a sloping plane at an angle of 45◦ .

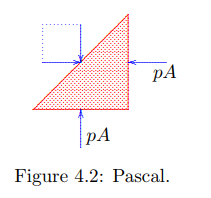If the pressure on the vertical plane at the right is p, the force on that plane is pA, where A is the area of that plane. Because there is no shear stress on the lower horizontal plane, the horizontal force pA must be equilibrated by a force component on the sloping plane. That component must therefore also be pA. Because on this plane also the shear stress is zero, it follows that there must also be a vertical force pA, so that the resulting force on the plane is perpendicular to it. This vertical force must be in equilibrium with the vertical force on the lower horizontal plane of the element. Because the area of that element is also A, the pressure on that plane is p, equal to the pressure on the vertical plane. Using a little geometry it can be shown that this pressure p acts on every plane through the same point. This is often denoted as Pascal’s principle. If the water is at rest (i.e. when there is no flow of the water), the pressure in the water is determined by the location of the point considered with respect to the water surface. As shown by Stevin the magnitude of the water pressure on the bottom of a container filled with water,

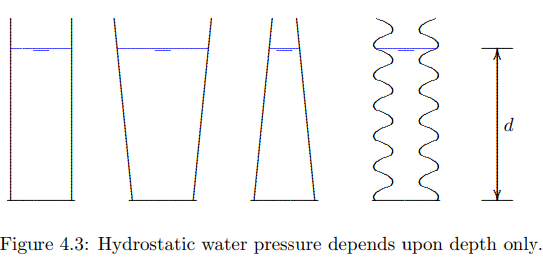
depends only upon the height of the column of water and the volumetric weight of the water, and not upon the shape of the container, see Figure 4.3. The pressure at the bottom in each case is

where γw is the volumetric weight of the water, and d is the depth below the water surface. The total vertical force on the bottom is γwdA. Only in case of a container with vertical sides this is equal to the total weight of the water in the container. Stevin showed that for the other types of containers illustrated in Figure 4.3 the total force on the bottom is also γwdA is. That can be demonstrated by considering equilibrium of the water body, taking into account that the pressure in every point on the walls must always be perpendicular to the wall. The container at the extreme right in Figure 4.3 resembles a soil body, with its pore space. It can be concluded that the water in a soil satisfies the principles of hydrostatics, provided that the water in the pore space forms a continuous body.