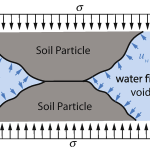
On an element of soil normal stresses as well as shear stresses may act. The simplest case, however, is the case of an isotropic normal stress, see Figure 4.4. It is assumed that the magnitude of this stress, acting in all directions, is σ. In the interior of the soil, for instance at a cross section in the center, this stress is transmitted by a pore presure p in the water, and by stresses in the particles. The stresses in the particles are generated partly by the concentrated forces acting in the contact points between the particles, and partly by the pressure in the water, that almost completely surrounds the particles. It can be expected that the deformations of the particle skeleton are almost completely determined by the concentrated forces in the contact points, because the structure can deform only by sliding and rolling in these contact points.

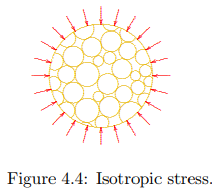The pressure in the water results in an equal pressure in all the grains. It follows that this pressure acts on the entire surface of a cross section, and that by subtracting p from the total stress σ a measure for the contact forces is obtained. It can also be argued that when there are no contact forces between the particles, and a pressure p acts in the pore water, this same pressure p will also act in all the particles, because they are completely surrounded by the pore fluid. The deformations in this case are the compression of the particles and the water caused by this pressure p. Quartz and water are very stiff materials, having elastic moduli about 1/10 of the elastic modulus os steel, so that the deformations in this case are very small (say 10−6 ), and can be disregarded with respect to the large deformations that are usually observed in a soil (10−3 to 10−2 ). These considerations indicate that it seems meaningful to introduce the difference of the total stress σ and the pore pressure p,

The quantity σ 0 is denoted as the effective stress. The effective stress is a measure for the concentrated forces acting in the contact points of a granular material. If p = σ it follows that σ 0 = 0, which means that then there are no concentrated forces in the contact points. This does not mean that the stresses in the grains are zero in that case, because there will always be a stress in the particles equal to the pressure in the surrounding water. The basic idea is, as stated above, that the deformations of a granular material are almost completely determined by changes of the concentrated forces in the contact points of the grains, which cause rolling and sliding in the contact points. These are described (on the average) by the effective stress, a concept introduced by Terzaghi. Eq. (4.2) can, of course, also be written as

Terzaghi’s effective stress principle is often quoted as “total stress equals effective stress plus pore pressure”, but it should be noted that this applies only to the normal stresses. Shear stresses can be transmitted by the grain skeleton only.

It may be noted that the concept is based upon the assumption that the particles are very stiff compared to the soil as a whole, and also upon the assumption that the contact areas of the particles are very small. These are reasonable assumptions for a normal soil, but for porous rock they may not be valid. For rock the compressibility of the rock must be taken into account, which leads to a small correction in the formula.

 To generalize the subdivision of total stress into effective stress and pore pressure it may be noted that the water in the pores cannot contribute to the transmission of shear stresses, as the pore pressure is mainly isotropic. Even though in a flowing fluid viscous shear stresses may be developed, these are several orders of magnitude smaller than the pore pressure, and then the shear stresses than may occur in a soil. This suggests that the generalization of (4.3) is

This is usually called the principle of effective stress. It is one of the basic prinicples of soil mechanics. The notation, with the effective stresses being denoted by an accent, σ 0 , is standard practice. The total stresses are denoted by σ, without accent.

 Even though the equations (4.4) are very simple, and may seem almost trivial, different expressions may be found in some publications especially relations of the form σ = σ 0 + np, in which n is the porosity. The idea behind this is that the pore water pressure acts in the pores only, and that therefore a quantity np must be subtracted from the total stress σ to obtain a measure for the stresses in the particle skeleton.

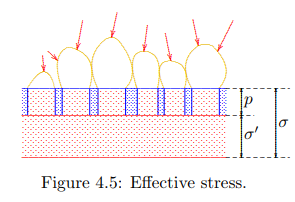That seems to make sense, and it may even give a correct value for the average stress in the particles, but it ignores that soil deformations are not in the first place determined by deformations of the individual particles, but mainly by changes in the geometry of the grain skeleton. This average granular stress might be useful if one wishes to study the effect of stresses on the properties of the grains themselves (for instance a photo-elastic or a piezo-electric effect), but in order to study the deformation of soils it is not useful. Terzaghi’s notion that the soil deformations are mainly determined by the contact forces only leads directly to the concept of effective stress, because only if one writes σ 0 = σ − p do the effective stresses vanish when there are no contact forces. The pore pressure must be considered to act over the entire surface to obtain a good measure for the contact forces, see Figure 4.5. The equations (4.4) can be written in matrix notation as

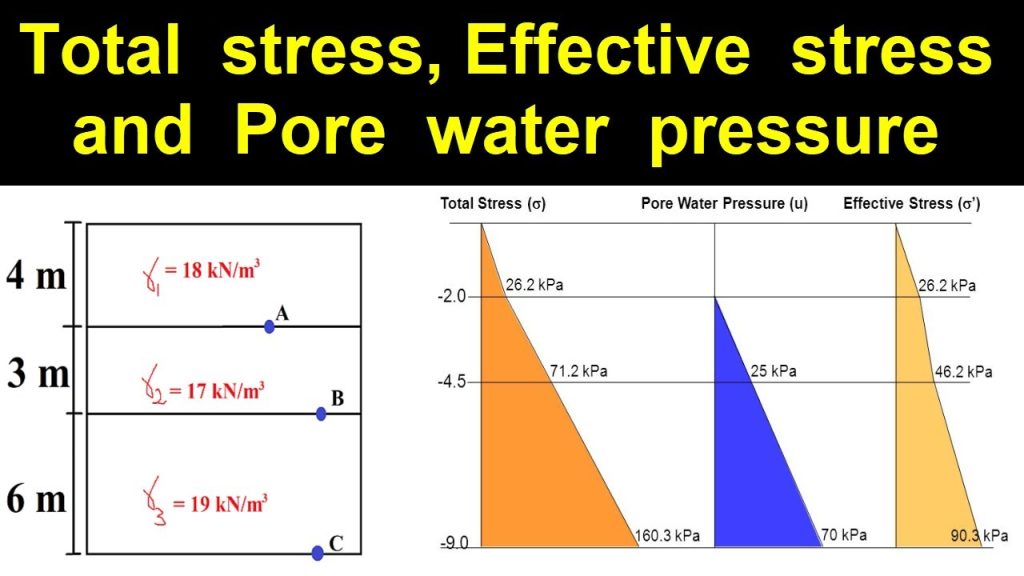
Calculating the effective stresses in soils is one of the main problems of soil mechanics. The effective stresses are important because they determine the deformations.