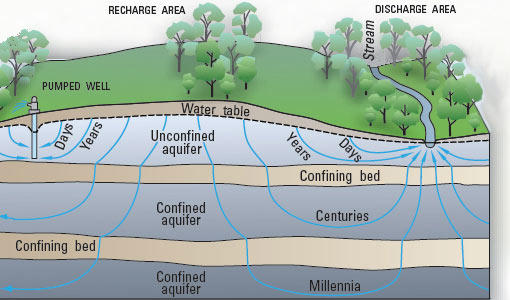
The hydrostatic distribution of pore pressures is valid when the groundwater is at rest. When the groundwater is flowing through the soil the pressure distribution will not be hydrostatic, because then the equations of equilibrium (6.1) are no longer complete. The flow of groundwater through the pore space is accompanied by a friction force between the flowing fluid and the soil skeleton, and this must be taken into account.

This friction force (per unit volume) is denoted by f. Then the equations of equilibrium are

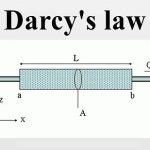
Here fx, fy and fz are the components of the force, per unit volume, exerted onto the soil skeleton by the flowing groundwater. The sign of these terms can be verified by considering the equilibrium in one of the directions, say the x-direction, see Figure 6.3. If the pressure increases in x-direction there must be a force in positive x-direction acting on the water to ensure equilibrium. Both terms in the equation of equilibrium then are positive, so that they cancel. It may be mentioned that in the equations the accelerations of the groundater might also be taken into account. This could be expressed by terms of the form ρax, ρay en ρaz in the right hand sides of the equations. Such terms are usually very small, however. It may be noted that the velocity of flowing groundwater usually is of the order of magnitude of 1 m/d, or smaller. If such a velocity would be doubled in one hour the acceleration would be (1/24) × (1/3600)2 m/s 2 , which is extremely small with respect to the acceleration of gravity g, which also appears in the equations. In fact the acceleration terms would be a factor 3 × 108 smaller, and therefore may be neglected.

It seems probable that the friction force between the particles and the water depends upon the velocity of the water, and in particular such that the force will increase with increasing velocity, and acting in opposite direction. It can also be expected that the friction force will be larger, at the same velocity, if the viscosity of the fluid is larger (the fluid is then more sticky). From careful measurements it has been established that the relation between the velocity and the friction force is linear, at least as a very good first approximation. If the soil has the same properties in all directions (i.e. is isotropic) the relations are

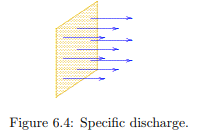
Here qx, qy and qz are the components of the specific discharge, that is the discharge per unit area. The precise definition of qx is the discharge (a volume per unit time) through a unit area perpendicular to the x-direction, qx = Q/A, see Figure 6.4. This quantity is expressed in m3/s per m2 , a discharge per unit area. In the SI-system of units that reduces to m/s. It should be noted that this is not the average velocity of the groundwater, because for that quantity the discharge should be divided by the area of the pores only, and that area is a factor n smaller than the total area. The specific discharge is proportional to the average velocity, however,

The fact that the specific discharge is expressed in m/s, and its definition as a discharge per unit area, may give rise to confusion with the velocity. This confusion is sometimes increased by denoting the specific discharge q as the filter velocity, the seepgae velocity or the Darcian velocity. Such terms can better be avoided: it should be denoted as the specific discharge. It may be interesting to note that in the USA the classical unit of volume of a fluid is the gallon (3.785 liter), so that a discharge of water is expressed in gallon per day, gpd. An area is expressed in square foot (1 foot = 30 cm), and therefore a specific discharge is expressed in gallons per day per square foot (gpd/sqft). That may seem an antique type of unit, but at least it has the advantage of expressing precisely what it is: a discharge per unit area. There is no possible confusion with a velocity, which in the USA is usually expressed in miles per hour, mph.

 Equation (6.4) expresses that there is an additional force in the equations of equilibrium proportional to the specific discharge (and hence proportional to the velocity of the water with respect to the particles, as intended). The constant of proportionality has been denoted by µ/κ, where µ is the dynamic viscosity of the fluid, and κ is the permeability of the porous medium. The factor 1/κ is a measure for the resistance of the porous medium. In general it has been found that κ is larger if the size of the pores is larger. When the pores are very narrow the friction will be very large, and the value of κ will be small. Substitution of equations (6.4) into (6.3) gives

In contrast with equations (6.1), which may be used for an infintely small element, within a single pore, equations (6.6) represent an equation of equilibrium for an element containing a sufficiently large number of pores, so that the friction force can be represented with sufficient accuracy as a factor proportional to the average value of the specific discharge. It may be noted that the equations (6.6) are also valid when the volumetric weight γw is variable, for instance due to variations of salt content, or in the case of two fluids (e.g. oil and water) in the pores. That can easily be demonstrated by noting that these equations include the hydrostatic pressure distribution as the special case for zero specific discharge, i.e for the no flow case. The equations (6.6) can also be written as

These equations enable to determine the components of the specific discharge if the pressure distribution is known.

The equations (6.7) are a basic form of Darcy’s law. They are named after the city engineer of the French town Dijon, who developed that law on the basis of experiments in 1856. Darcy designed the public water works of the town of Dijon, by producing water from the ground in the center of town. He realized that this water could be supplied from the higher areas surrounding the town, by flowing through the ground. In order to assess the quantity that could be produced he needed the permeability of the soil, and therefore measured it. The grateful citizens of Dijon honoured him by erecting a statue, and by naming the central square the Place Henri Darcy.

The equations (6.7) are generally valid, also if the volumetric weight γw of the fluid is not constant. In civil engineering many problems are concerned with a single fluid, fresh water, and the volumetric weight can then be considered as constant. In that case it is convenient to introduce the groundwater head h, defined as

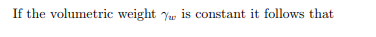
Using these relations Darcy’s law, eqs. (6.7), can also be written as

The quantity k in these equations is the hydraulic conductivity, defined as

It is sometimes denoted as the coefficient of permeability. The permeability κ then should be denoted as the intrinsic permeability to avoid confusion.

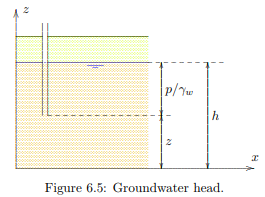
Darcy himself wrote his equations in the simpler form of eq. (6.10). For engineering practice that is a convenient form of the equations, because the groundwater head h can often be measured rather simply, en because the equations are of a simple character, and are the same in all three directions. It should be remembered, however, that the form 6.7 is more fundamentally correct. If the volumetric weight γw is not constant, only the equations (6.7) can be used. The definition (6.8) then does not make sense. The concept of groundwater head can be illustrated by considering a standpipe in the soil, see Figure 6.5. The water level in the standpipe, measured with respect to a certain horizontal level where z = 0, is the groundwater head h in the point indicated by the open end of the standpipe. In the standpipe the water is at rest, and therefore the pressure at the bottom end of the pipe is p = (h−z)γw, so that h = z +p/γw, in agreement with (6.8). When the groundwater head is the same in every point of a soil mass, the groundwater will be at rest. If the head is not constant, however, the groundwater flow, and according to eq. (eq:darcy:qh) it will flow from locations with a large head to locations where the head is low. If the groundwater flow is not maintained by some external influence (rainfall, or wells) the water will tend towards a situation of constant head. Darcy’s law can be written in an even simpler form if the direction of flow is known, for instance if the water is flowing through a narrow tube, filled with soil. The water is then forced to flow in the direction of the tube. If that directions is the s-direction, the specific discharge in that direction is, similar to (6.10).

The quantity dh/ds is the increase of the groundwater head per uint of length, in the direction of flow. The minus sign expresses that the water flows in the direction of decreasing head. This is the form of Darcy’s law as it is often used in simple flow problems. The quantity dh/ds is called the hydraulic gradient i,

It is a dimensionless quantity, indicating the slope of the phreatic surface.