In the previous chapter it has been seen that under certain conditions the effective stresses in the soil may be reduced to zero, so that the soil loses its coherence, and a structure may fail. Even a small additional load, if it has to be carried by shear stresses, can lead to a calamity. Many examples of failures of this type can be given : the bursting of the bottom of excavation pits, and the floatation of basements, tunnels and pipelines. The floatation of structures is discussed in this chapter.
Archimedes
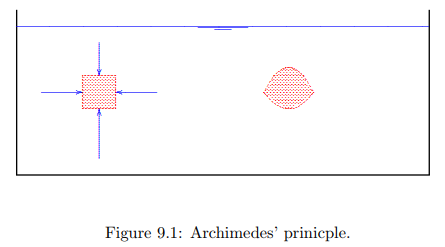
The basic principle of the uplift force on a body submerged in a fluid is due to Archimedes. This principle can best be understood by considering a small rectangular element, at rest in a fluid, see Figure 9.1. The material of the block is irrelevant, but it must be given to be at rest. The pressure in the fluid is a function of depth only, and in a homogeneous fluid the pressure distribution is

where ρ is the density of the fluid, g the acceleration of gravity, and z the depth below the fluid surface.
The pressures on the left hand side and the right hand side are equal, but act in opposite direction, and therefore are in equilibrium. The pressure below the element is greater than the pressure above it. The resultant force is equal to the difference in pressure, multiplied by the area of the upper and lower surfaces. Because the pressure difference is just ρgh, where h is the height of the element, the upward force equals ρg times the volume of the element. That is just the volumetric weight of the water multiplied by the volume of the element. Because any body can be constructed from a number of such elementary blocks, the general applicability of Archimedes’ prinicple follows.
A different argument, that immediately applies to a body of arbitrary shape, is that in a state of equilibrium the precise composition of a body is irrelevant for the force acting upon it. This means that the force on a body of water must be the same as the force on a body of some other substance, that then perhaps must be kept in equilibrium by some additional force. Because the body when composed of water is in equilibrium it follows that the upward force must be equal to the weight of the water in the volume. On a body of some other substance the resultant force of the water pressures must be the same, i.e. an upward force equal to the weight of the water in the volume. This is the proof that is given in most textbooks on elementary physics. The upward force is often denoted as the buoyant force, and the effect is denoted as buoyancy.
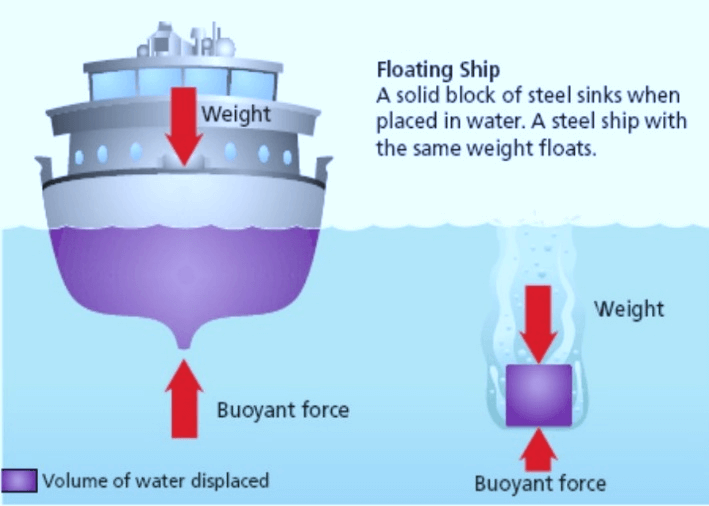
The buoyancy force on a body in a fluid may have as a result that the body floats on the water, if the weight of the body is smaller than the upward force. Floatation will happen if the body on the average is lighter than water. More generally, floatation may occur if the buoyancy force is larger than the sum of all downward forces together. This may happen in the case of basements, tunnels, or pipelines. In principle floatation can easily be prevented: the body must be heavy enough, and may have to be ballasted.
The problem of possible floatation of a foundation is that care must be taken that the effective stresses are always positive, taking into account a certain margin of safety. In practice this may be more difficult than imagined, because perhaps not all conditions have been foreseen. Some examples may illustrate the analysis.