The notion that failure of a soil occurs by sliding along a plane on which the shear stress reaches a certain maximum value has lead to the development of shear tests. In such tests a sample is loaded such that it is expected that one part of the asmple slides over another part, along a given sliding plane. It is often assumed that the sliding plane is fixed and given by the geometry of the equipment used, but it will appear that the deformation mode may be more complicated.
Direct shear test
The simplest apparatus is shown in Figure 22.1. It consists of a box (the shear box ) of which the upper half can be moved with respect to the lower half, by means of a motor which pushes the lower part away from the upper part, which is fixed in horizontal direction. The cross section
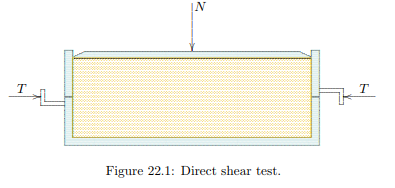
of the container usually is rectangular, but circular versions also exist. The soil sample is loaded initially by a vertical force only, applied by the dead weight of a loading plate and some additional weights on it, through the intermediary of a small steel plate on top of the sample. Because of this plate the sample is free to deform in vertical direction during the test. The actual consists of the lateral movement of the lower half of the box with respect to the upper half, at a constant (small) speed, with a horizontal force acting in the plane between the two halves. This force gradually increases, as the box moves, and is measured by a pressure ring or a strain gauge. The horizontal force reaches a maximum value after some time, and the force remains more or less constant afterwards, or it may slowly increase or decrease. It seems logical to assume that the maximum value of the horizontal force (Tf ) is related to the vertical force N by a relation of the form

where A is the area of the sample, c is the cohesion of the material, and φ its friction angle. For simplicity it is assumed that the soil is dry sand, with c = 0. This means that a single test is sufficient to determine the friction angle φ.
Many investigators have found that the test results of shear tests lead to values for the shear strength that are considerably lower than the values obtained from triaxial tests. Furthermore, it has sometimes been found that the reproducibility of the results of shear tests is not so good. To explain the relatively large scatter in the results of shear tests it may be noted that in a shear test the horizontal stress is not imposed, and may vary from test to test. This may influence the test results, especially because it may be argued that it is not so certain that the stresses on a horizontal plane are indeed the critical stresses, as is assumed in equation (22.1). It may perhaps be possible that there is some other plane on which the critical state of stress is reached earlier. A likely candidate for this possibility is the vertical plane, on which the normal stress may well be smaller than on a horizontal plane, whereas the shear stress on a vertical plane is equal to the shear stress on a horizontal plane because of equilibrium of moments, σxz = σzx. In such a case the soil may fail according to the mechanism of the toppling row of books suggested by De Josselin de Jong, see Figure 22.2
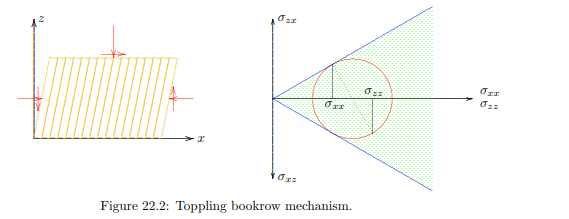
It seems very much likely that the horizontal normal stress σxx is smaller than the vertical normal stress σzz. If the sand has been poured into the shear box, and the vertical load has been applied by gradually increasing the load, it seems likely that the horizontal stress is smaller than the vertical stress. In an elastic material, for instance, the ratio of horizontal to vertical stress would be σxx/σzz = ν/(1 − ν), where ν is Poisson’s ratio, which must be smaller than 1 2 . If the shear stress now is gradually increased, the maximum possible shear stress on a vertical plane is smaller than the maximum possible shear stress on a horizontal plane. Thus it can be expected that the maximum possible shear stress is reached first on a vertical plane, so that failure may occur by sliding along a vertical plane, combined with a certain rotation in order to satisfy the boundary condition on the lower and upper horizontal boundaries. The stresses are indicated in the Mohr circle that is also drawn in Figure 22.2. It should be noted that in this case the shear stresses σxz and σzx, in the coordinate system assumed, will be negative. In the Mohr circle it has been assumed that σxx < σzz. Because the point with coordinates σxx and σxz is located to the left of the point with coordinates σzz and σzx, sliding will occur first along the planes on which the normal stress σxx is acting, i.e. the vertical planes. On the horizontal planes, i.e. the planes on which the normal stress is σzz, failure will not be reached, so that no sliding along these planes is to be expected. With the shear stresses acting in the direction indicated in the figure this means that the soil to the right of a vertical plane will slide in upwards direction with respect to the soil at the left side of that plane. In Figure 22.2 it has been assumed that such sliding occurs along a great number of vertical planes. In order to conform to the restrictions imposed by the deformation of the walls of the shear box, an additional rotation must be superimposed onto the sliding mechanism. This can be done without change of stress, as a rigid body rotation can occur without any deformation, and therefore requires no stresses. Thus the mechanism of a toppling book row is produced, just as a row of books in a book case will topple if there is insufficient lateral support. If it is desired to prevent the toppling of a row of books, a large lateral stress may be applied, which may be generated by two heavy bookends, or by clamping the books between the two sides of the book case. Using this analogy it may be considered that the mechanism of Figure 22.2 can be prevented by applying a high horizontal stress. If the horizontal normal stress is larger than the vertical normal stress, for instance because the sand has been densified by strong vibration, the state of stress on a horizontal plane will become critical before a vertical plane. The stresses σzx and σzz, acting on a horizontal plane, will reach the critical ratio tan φ before the stresses σxz and σxx, acting on a vertical plane. This means that sliding along horizontal planes can be expected if the horizontal stress is larger than the vertical stress. The situation
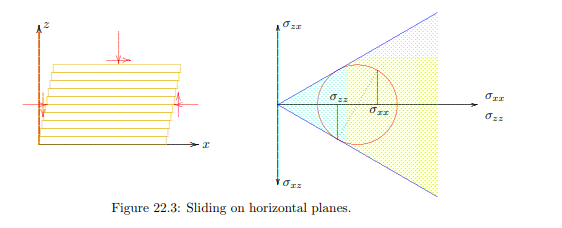
is shown in Figure 22.3. The Mohr circle for this case is also shown in the figure.


