If the theory of consolidation, presented in the previous chapters, were a perfect description of the physical behaviour of soils, it should be rather simple to determine the value of the coefficient of consolidation cv from the data obtained in a consolidation test. For instance, one could measure the time at which 50 % of the final deformation has taken place. From the theory it follows that this is reached when cvt/h2 = 0.197, because then the value of U = 0.5, see formula (16.19). As the values of time t and the sample thickness h are known, it is then possible to determine the value of cv. Unfortunately, there are some practical and some theoretical difficulties. The procedure would require an accurate determination of the intial deformation and of the ultimate deformation, and that is not so simple as it may seem. The initial deformation of the sample, ∆h0, is the deformation at the moment of application of the load, and at the moment of loading the indicator of the deformation will suddenly start to move, with a sudden jump followed by a continuous increase. It is difficult to decide what the value at the exact moment of loading is, as the moment is gone when the indicator starts to move. Also, it usually appears that no final constant value of the deformation, ∆h∞ is reached, as the deformation seems to continue, even when the pore water pressures have been dissipated completely. For these reasons somewhat modified procedures have been developed to define the initial deformation and the final deformation. In this chapter the two most common procedures are presented.

Log(t)-method

A first method to overcome the difficulties of determining the initial value and the final value of the deformation has been proposed by Casagrande. In this method the deformation of the sample, as measured as a function of time in a consolidation test, is plotted against the logarithm of time, see Figure 18.1. It usually appears that there is no horizontal asymptote of the curve, as the classical theory predicts, but for very large values of time a straight line is obtained. It is now postulated, somewhat arbitrarily, that the intersection point of the straight line asymptote for very large values of time, with the straight line that can be drawn tangent to the measurement curve at the inflection point (that is the steepest possible tangent), is considered to determine the final deformation of the primary consolidation process. The continuing deformation beyond that deformation is denoted as secondary consolidation, representing deformation at practically zero pore pressures. This procedure is indicated in Figure 18.1, leading to the value ∆h∞ for the final deformation. In order to define the initial settlement of the loaded sample use is made of the knowledge, see chapter 16, that in the beginning of the consolidation process the degree of consolidation increases proportional to √ t. This means that between t = 0 and t = t1 the deformation will be equal to the deformation between t = t1 and t = 4t1. If the deformation is measured after 1 minute and after 4 minutes, it can be assumed that between t = 0 and t = 1 minute the deformation would have been the same as the deformation between t = 1 minute and t = minutes. This procedure has been indicated in Figure 18.1, leading to the value ∆h0 for the initial deformation.

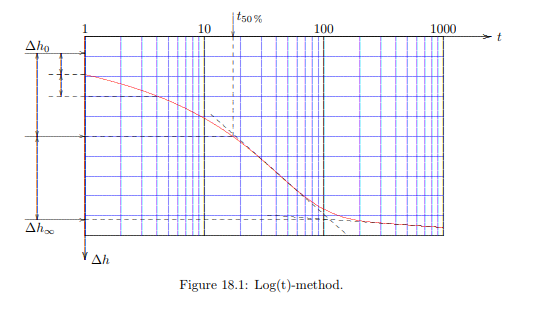
From the values of the initial deformation ∆h0 and the final deformation ∆h∞, it is simple to determine the moment at which the degree of consolidation is just between these two values, which would mean that U = 0.5. This is also indicated in Figure 18.1, giving a value for t50 %. The value of the coefficient of consolidation then follows from cvt50 %/h2 = 0.197, or

It should be noted that the quantity h in this expression represents the thickness of the sample, for the case of a sample drained on one side only. The consolidation process would be the same in a sample of thickness 2h and drainage to both sides. The original solution of Terzaghi considers that case, and it can be found in many textbooks. Because of the symmetry of that problem there is no difference with the problem and the solution considered here.