Potential and stream function
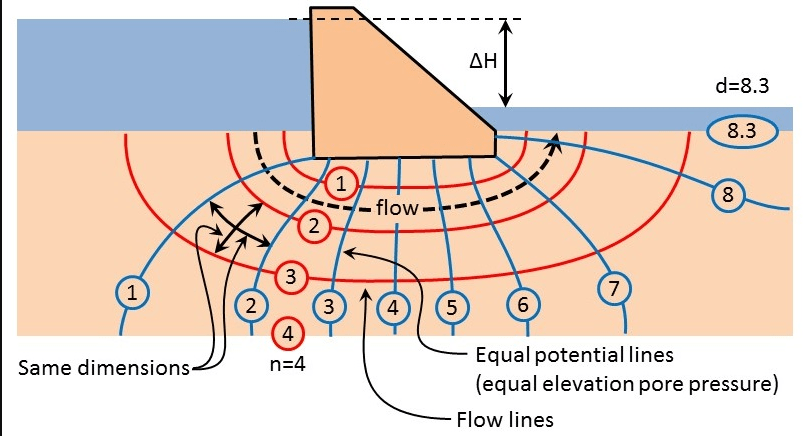
Two dimensional groundwater flow through a homogeneous soil can often be described approximately in a relatively simple way by a flow net, that is a net of potential lines and stream lines
The groundwater potential, or just simply the potential, Φ is defined as

where k is the permeability coefficient (or hydraulic conductivity), and h is the groundwater head. It is assumed that the hydraulic conductivity k is a constant throughout the field. If this is not the case the concept of a potential can not be used. Darcy’s law, see (8.1), can now be written as
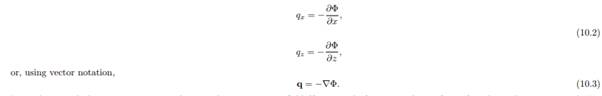
In mathematical physics any quantity whose gradient is a vector field (for example forces or velocities), is often denoted as a potential. For that reason in groundwater theory Φ is also called the potential. In some publications the groundwater head h itself is sometimes called the potential, but strictly speaking that is not correct, even though the difference is merely the constant k.
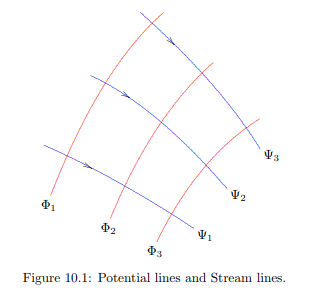
The equations (10.2) indicate that no groundwater flow will flow in a direction in which the potential Φ is not changing. This means that in a figure with lines of constant potential (these are denoted as potential lines) the flow is everywhere perpendicular to these potential lines, see Figure 10.1.
The flow can also be described in terms of a stream function. This can best be introduced by noting that the flow must always satisfy the equation of continuity, see (8.2), i.e.

This means that a function Ψ must exist such that

By the definition of the components of the specific discharge in this way, as being derived from this function Ψ, the stream function, the continuity equation (10.4) is automatically satisfied, as can be verified by substitution of eqs. (10.5) into (10.4).
It follows from (10.5) that the flow is precisely in x-direction if the value of Ψ is constant in x-direction. This can be checked by noting that the condition qz = 0 can only be satisfied if ∂Ψ/∂x = 0. Similarly, the flow is in z-direction only if Ψ is constant in z-direction, beacuse it follows that qx = 0 if ∂Ψ/∂z = 0. This suggests that in general the stream function Ψ is constant in the direction of flow. Along the stream lines in Figure 10.1 the value of Ψ is constant. Formally this property can be proved on the basis of the total differential

This will be zero if dz/dx = qz/qx, and that means that the direction in which dΨ = 0 is given by dz/dz = qz/qx, which is precisely the direction of flow. It can be concluded that in a mesh of potential lines and stream lines the value of Ψ is constant along the stream lines. If the x-direction coincides with the direction of flow, the value of qz is 0. It then follows from (10.2) and (10.5) that in that case Φ is constant in z-direction, and that Ψ is constant in x-direction. Furthermore, in that case one may write, approximately

It now follows that if the intervals ∆Φ and ∆Ψ are chosen to be equal, then ∆x = ∆z, i.e. the potential line and the stream line locally form a small square. That is a general property of the system of potential lines and streamlines (the flow net): potential lines and stream lines form a system of ”squares”.
The physical meaning of ∆Φ can be derived immediately from its definition, see equation 10.2. If the difference in head between two potential lines, along a stream line, is ∆h, then ∆Φ = k∆h. The physical meaning of ∆Ψ can best be understood by considering a point in which the flow is in x-direction only. In such a point q = qx = −∆Ψ/∆z, or ∆Ψ = −q ∆z. In general one may write

where n denotes the direction perpendicular to the flow direction, with the relative orientation of n and s being the same as for z and x. If the thickness of the plane of flow is denoted by B, the area of the cross section between two stream lines is ∆nB. It now follows that

The quantity ∆Ψ appears to be equal to the discharge per unit thickness being transported between two stream lines. It will appear that this will enable to determine the total discharge through a system.