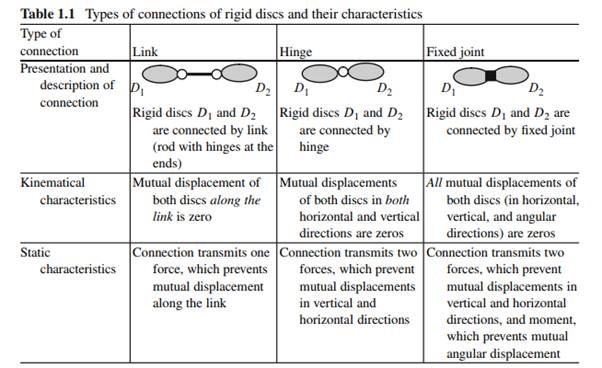
Kinematical analysis of a structure is necessary for evaluation of ability of the structure to resist external load. Kinematical analysis is based on the concept of rigid disc, which is an unchangeable (or rigid) part of a structure. Rigid discs may be separate members of a structure, such as straight members, curvilinear, polygonal (Fig. 1.1), as well as their special combination. Any structure consists of separate rigid discs. Two rigid discs may be connected by means of link, hinge, and fixed joint. These types of connections and their static and kinematical characteristics are presented in Table 1.1. The members of a structure may be connected together by a hinge in various ways. Types of connection are chosen and justified by an engineer as follows:
1. Simple hinge. One hinge connects two elements in the joint.
2. Multiple hinge. One hinge connects three or more elements in the joint. The multiple hinge is equivalent to n–1 simple hinges, where n is a number of members connected in the joint. Hinged joints can transmit axial and shear forces from one part of the structure to the other; the bending moment at the hinge joint is zero.
Classification of Structures by Kinematical Viewpoint
All structures may be classified as follows:
· Geometrically unchangeable structure. For this type of structure, any distortion of the structure occurs only with deformation of its members. It means that this type of structure with absolutely rigid members cannot change its form. The simplest geometrically unchangeable structure is triangle, which contains the pin-joined members (Fig. 1.2a).
· Geometrically changeable structure. For this type of structure, any finite distortion of the structure occurs without deformation of its members. The simplest geometrically changeable system is formed as hinged four-bar linkage (Fig. 1.2b, c). In Fig. 1.2c, the fourth bar is presented as ground. In both cases, even if the system would be made with absolutely rigid members, it still can change its form
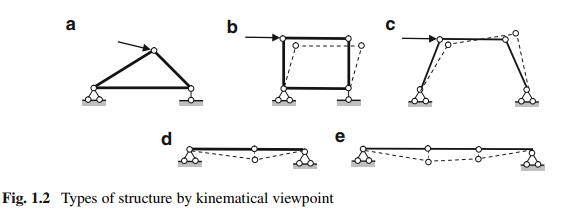
It is pertinent to do the following important remark related to terminology. Sometimes terms “stable” and “unstable” are applied for the above-mentioned types of structures. However, the commonly accepted term “stable/unstable” in classical theory of deformable systems is related to concept of critical load, while term “geometrically unchangeable/changeable” is related to way of connection of rigid disks. There is the fundamental difference between kinematical analysis of a structure on the one hand, and analysis of stability of a structure subjected to compressed load, on the other hand. Thus, in kinematical analysis of structures, we will use the term “unchangeable structure” instead of “stable structure,” and term “changeable structure” instead of “unstable structure.”
· Instantaneously changeable structure. This system allows infinitesimal relative displacements of its members without their deformation and after that the structure becomes geometrically unchangeable (Fig. 1.2d).
· Instantaneously rigid structure. This system allows infinitesimal relative displacements of its members without their deformation and after that the structure becomes geometrically changeable (Fig. 1.2e). The term “instantaneously” is related to initial condition of the structure only.
In structural engineering only geometrically unchangeable structures may be accepted.