Construction of influence lines for one span simply supported and cantilevered beams in case of direct and indirect load applications are considered. All influence lines are constructed using analytical expressions for required factor. Applications of influence lines for fixed and moving loads are discussed. This chapter forms the set of concepts which creates a framework for comprehensive analysis of different statically determinate structures.

Analytical Method for Construction of Influence Lines

The engineering structures are often subjected to moving loads. Typical examples of moving loads on a structure are traveling cars, trains, bridge cranes, etc. In classical structural analysis, the term “moving load” requires one additional comment: this concept means that only the load position on the structure may be arbitrary.

It is obvious that internal forces and displacements in any section of a beam depend on the position of a moving load. An important problem in analysis of structures is the determination of maximum internal forces in a structure caused by a given moving load and the corresponding most unfavourable position of this load. This problem may be solved using influence lines. Influence line is a fundamental and very profitable concept of structural analysis. Their application allows perform a deep and manifold analysis of different types of structures subjected to any type of fixed and moving loads. Influence lines method becomes especially effective tool analysis if a structure is subjected to different groups of loads.

Definition:

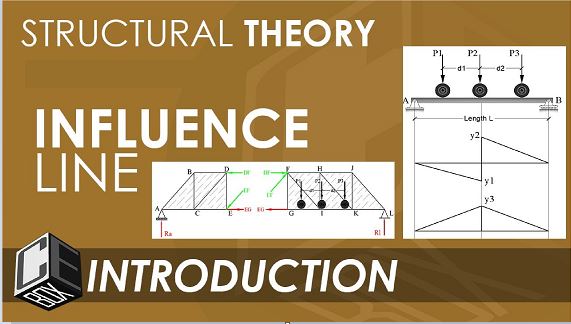
Influence line is a graph, which shows variation of some particular function Z (reaction, shear, bending moment, etc.) in the fixed cross section of a structure in terms of position of unit concentrated dimensionless load P D 1 on the structure.

Each ordinate of influence line means the value of the function, for which influence line is constructed, if the unit load is located on the structure above this ordinate. Therefore, the unit load P, which may have different positions on the structure, is called a moving (or traveling) load. The term “moving load” implies only that position of the load is arbitrary, i.e., this is a static load, which may have different positions along the beam. The time, velocity of the moving load, and any dynamic effects are not taken into account. Thus, for convenience, from now on, we will use notion of “moving” or “traveling” load for static load, which may have different position along the beam. Influence line for any function Z at a specified section of a structure may be constructed using its definition as follows: the required function should be calculated for different position of unit load within the loaded portion. These values are plotted at the points, which correspond to the position of the load. After that all ordinates should be connected. However, such procedure is extremely annoying and cumbersome (especially for statically indeterminate structures). Because of repetitive procedure of construction of influence lines, their advantages are questionable.

The construction of influence lines is performed on the bases of a different approach, i.e., deriving an equation of influence line for required function Z; this equation relates values of Z and position x of the unit load P. Thus the required factor Z is presented as analytical function of the position of the load. Such way of construction of influence lines is called static method. Application of this method for construction of influence lines for reactions is presented below.