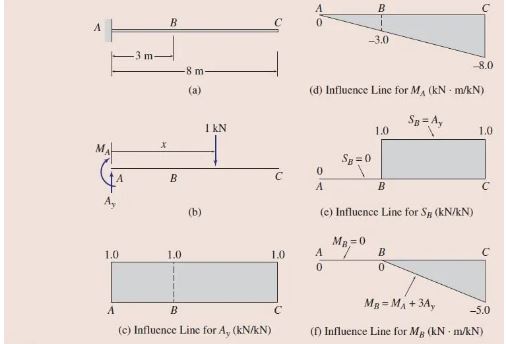
The following types of beams are considered: simply supported beam, beam with overhang, and cantilever beam.
Simply Supported Beam (Fig. 2.1)
The beam AB is loaded by moving load P D 1. The moving load is shown by circle and the dotted line indicates the loaded contour for possible positions of the load on the structure The distance from the left-hand support to the load is x.
Influence Line for RA
Equilibrium equation in form of moments of all external forces about the support B allows determine the reaction RA in terms of x:
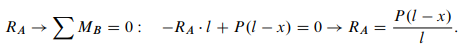
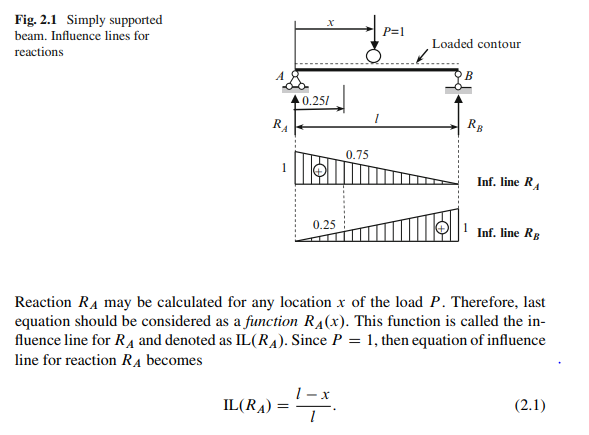
If x = 0 (at support A), then ordinate of influence line IL.RA = 1. If x = l (at support B), then ordinate of influence line IL.RA/ = 0. These two points are connected by straight line, since function (2.1) is linear. Influence line for RA is presented in Fig. 2.1. We can see that units of influence line ordinates for reaction is dimensionless. In general, units of influence line ordinates for any factor Z are defined as quotient of two units, mainly, unit of the factor Z and unit of the load P (kN). Thus, unit of influence line for reactions and shear is dimensionless because kN/kN; for bending moment: kN m/kN D m; for linear deflection m/kN; for angular deflection rad/kN.
Influence line IL.RA/ can be used for analysis of reaction RA only. Positive ordinates mean that reaction of RA is directed upward for any position of the concentrated load. If load P = 1 is located above point A, then reaction of RA is equal to 1; it means that load P completely transmits on the support A. If load P = 1 is located above point B, then reaction of RA is equal to zero. If load P = 1 has, for example, coordinate x = 0:25l, then reaction of RA is equal to 0.75.
Analytical presentation of equation of influence line allows to avoid many times repeated computation of function Z for different location of the force P; this is a huge advantage of analytical approach for construction of influence lines. Note a following fundamental property: influence lines for reactions and internal forces of any statically determined structures are always presented by straight lines.

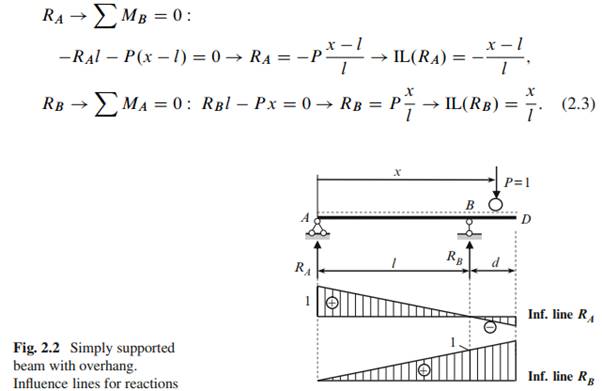
Simply Supported Beam with Overhang (Fig. 2.2)
The equilibrium equations and corresponding equations for influence lines of reactions are

Cantilevered Beam (Fig. 2.3)