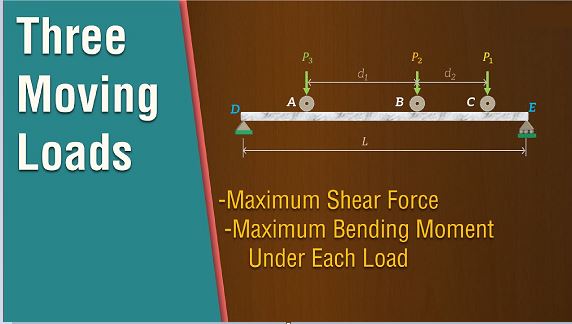
Influence line for any function Z allows us to calculate Z for any position of a moving load, and that is very important, the most unfavourable position of the moving loads and corresponding value of the relevant function. Unfavourable (or dangerous) position of a moving load is such position, which leads to the maximum (positive or negative) value of the function Z. The following types of moving loads will be considered: one concentrated load, a set of loads, and a distributed load.
The set of connected moving loads may be considered as a model of moving truck. Specifications for truck loading may be found in various references, for example in the American Association of State and Highway Transportation Officials (AASHTO). This code presents the size of the standard truck and the distribution of its weight on each axle. The moving distributed load may be considered as a model of a set of containers which may be placed along the beam at arbitrary position.
The most unfavourable position of a single concentrated load is its position at a section with maximum ordinate of influence line. If influence line has positive and negative signs, then it is necessary to calculate corresponding maximum of the function Z using the largest positive and negative ordinates of influence lines.
In case of set of concentrated moving loads, we assume that some of loads may be connected. This case may be applicable for moving cars, bridge cranes, etc. We will consider different forms of influence line.
Influence Line Forms a Triangle
A dangerous position occurs when one of the loads is located over the vertex of an influence line; this load is called a critical load. (The term “critical load” for problems of elastic stability, Chap. 13, has a different meaning.) The problem is to determine which load among the group of moving loads is critical. After a critical load is known, all other loads are located according to the given distances between them.
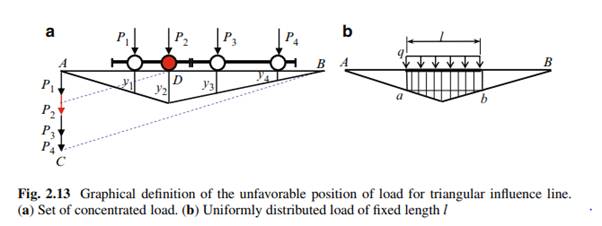
The critical load may be easy defined by a graphical approach (Fig. 2.13a). Let the moving load be a model of two cars, with loads Pi on the each axle. All distance between forces are given.
Step 1. Trace the influence line for function Z. Plot all forces P1, P2, P3, P4 in order using arbitrary scale from the left-most point A of influence line; the last point is denoted as C.
Step 2. Connect the right most point B with point C.
Step 3. On the base line show the point D, which corresponds to the vertex of influence line and from this point draw a line, which is parallel to the line CB until it intersection with the vertical line AC.
Step 4. The intersected force (in our case P2) presents a critical load; unfavourable location of moving cars presented in Fig. 2.13a
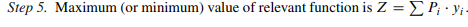
Influence Line Forms a Polygon
A dangerous position of the set of moving concentrated loads occurs when one or more loads stand over vertex of the influence line. Both, the load and the apex of the influence line over which this load must stand to induce a maximum (or minimum) of the function under consideration, are called critical. The critical apex of the influence line must be convex.
In case of Uniformly distributed moving load, the maximum value of the function Z corresponds to the location of a distributed load q, which covers maximum one sign area of influence line. The negative and positive portions of influence line must be considered in order to obtain minimum and maximum of function Z.
The special case of uniformly distributed moving load happens, if load is distributed within the fixed length l. In case of triangular influence line, the most unfavourable location of such load occurs when the portion ab D l and base AB will be parallel (Fig. 2.13b).