The trusses according to their generation are subdivided into simple, compound, and complex ones.

Simple Trusses

Simple trusses are formed on the basis of a hinge-connected triangle with any additional joint attached by means of two additional members. The relationship between the number of bars (S) and joints (J ) for simple statically determined and geometrically unchangeable trusses is expressed as

Thus, the two different approaches both lead to the same (3.1) for the kinematical analysis of a simple truss. Therefore, if a simple truss is statically determinate, its geometry must be unchangeable and vice versa. Note, however, that (3.1), while necessary, is an insufficient condition on its own to determine that a truss is geometrically unchangeable. It is indeed possible to devise a structure which satisfies (3.1) yet connects the bars in such a way that the structure is geometrically changeable. For more examples see Chap. 1.

If the number of bars S > 2J 3, then the system is statically indeterminate; this case will be considered later in Part 2. If the number of bars S < 2J 3, then the system is geometrically changeable and cannot be used as an engineering structure.

Compound Trusses

A compound truss consists of simple trusses connected to one another. There are different ways to connect simple trusses in order to construct a compound truss.

First approach uses three hinges, not arranged in line. Such an interconnection can be considered as a simple triangle on the basis of its three rigid discs. In the examples below, two of the trusses are represented by disks D1 and D2 (Fig. 3.8). Two immovable (pinned) supports may be treated as rigid disk D3 (the earth).

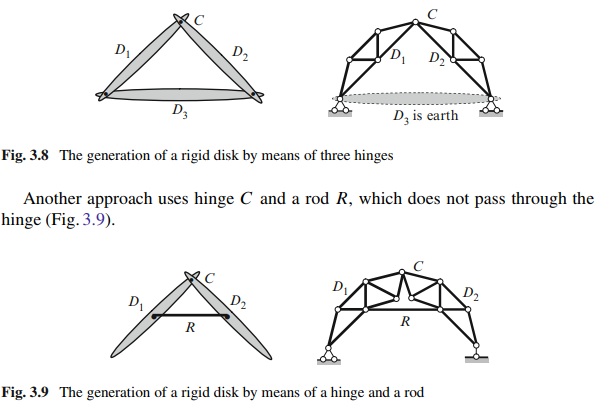
A third method uses three rods, which are not parallel and do not all intersect at the same single point (Fig. 3.10).

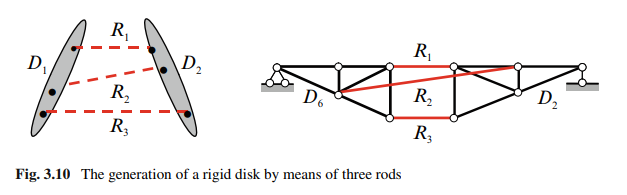
In addition, compound trusses can be composed of members that are themselves also trusses (Fig. 3.11). Such trusses suit structures carrying considerable loads, in which the truss designs would require heavy solid members. In these cases it is often more efficient to replace solid members with truss members.

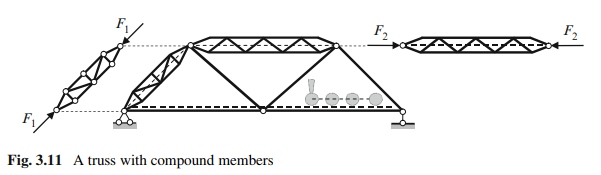
The analysis of this truss should be performed as if all the compounded members are solid rods. The obtained internal forces should be applied to the compound member and then that member is considered as a truss. Since each compound member is subjected to two balanced forces, the reactions of the supports are each zero. Therefore, the supports of each compound member can be disregarded.