Highway bridges have the main objective of carrying traffic; therefore traffic loading is a primary source of stress on the structure – quite often the largest one. However, traffic conditions are rather variable, as they depend on many factors, ranging from the macroscale (such as economic development) to the microscale (such as individual driver behaviour). While the resistance of bridges has been fairly well studied, less attention has been paid to the load to which a bridge is actually exposed.
Not surprisingly, the weight of heavy vehicles is of particular interest in traffic loading. Maximum weights are regulated by national governments and the truck weight allowance has constantly increased over the years. Not only have the single truck weights increased, but also the number of trucks on the road has steadily grown. Furthermore, overloaded and non-regulated trucks are not such rare events. Therefore, while the road infrastructure is inevitably deteriorating, the load to which it is exposed is globally increasing.
To account for the large variability of vehicle weights and traffic conditions, codes of practice prescribe fairly conservative load models for the design of new bridges, whereas only few codes are available for the assessment of existing bridges. Furthermore, the vast majority of codes are limited to short and medium spans.
On the contrary, most bridges are not likely to experience the high level of load prescribed in the design codes, with the consequence that the applied design load models may be disproportionate to the traffic that the bridge actually carries. This approach is generally acceptable for new bridges, for which an increase in load typically requires a less than proportionate increase in construction costs, whereas in the case of existing bridges it may play a decisive role in planning maintenance operations [1]. This may even result in the bridge being replaced unnecessarily or prematurely.
It is therefore apparent that the safety conditions of existing bridges need to be carefully reassessed to avoid unsafe situations or else unnecessary maintenance. Nowadays, it is relatively easy to obtain information on the traffic expected to occur on an existing bridge. The use of such site-specific traffic data may enable tailored maintenance operations, thus leading to an optimal – yet safe – use of the infrastructure. Significant savings can be achieved in both economic and environmental terms (e.g. saved maintenance costs and material production, or avoided congestion due to traffic disruptions).
RESEARCH ON HIGHWAY BRIDGE TRAFFIC LOADING
Research in bridge loading is often related to the development of codes or standards. In the context of bridge loading, it is convenient to define a short-span bridge as a bridge whose governing traffic case is free-flowing traffic plus an allowance for dynamic effects, as opposed to a long-span bridge, which is governed by congested traffic with no dynamic effects. The bridge length threshold between the two cases depends on many factors but it is currently thought to lie between 30 and 50 m.
Research on highway bridge traffic loading has mainly focussed on short-span bridges. For those bridges, The governing traffic case typically consists of or two big vehicles in free-flowing conditions, which dynamically interact with the bridge. No cars are involved in the governing case; hence, data about individual heavy vehicles generally suffice. This information is nowadays commonly available from Weigh-In-Motion (WIM) stations, often paired with inductive loop detectors. Importantly, recent studies have shown that the dynamic increment for extreme loading events may not be as high as previously thought [2, 3]. This has the potential of lowering the above-mentioned threshold between the two governing traffic states [4].
In contrast, long-span bridge loading is governed by congested traffic. Vehicles strongly interact with each other and driver behaviour becomes relevant. Cars cannot be neglected, as they play an important indirect role by keeping heavy vehicles apart. Unfortunately, there is a long-standing shortage of congested traffic data, mainly due to current limitations of detection techniques. This is reflected in the fact that most existing long-span bridge traffic load models are based on conservative assumptions, such as a queue of vehicles at minimum bumper-to-bumper distances [5–11], thus neglecting driver behaviour. However, traffic-related technologies are developing rapidly, thus enabling a better understanding of driver behaviour and overall traffic features, particularly during congestion. It is therefore sensible to introduce both recent and consolidated advances in traffic modelling into bridge-loading research. Among those, traffic microsimulation is a powerful tool to simulate realistic congested scenarios, based on widely available free-traffic measurements. Furthermore, increased computer performance allows for the simulation of the long periods required to identify extreme loading events.
METHODOLOGY
In general, the process to compute site-specific bridge traffic loading consists of the following steps:
1. Traffic data collection: This provides the basis for the analysis. It traditionally includes truck weight and axle data, and more recently vehicle speed and time headways, generally sufficient for short-span bridges. However, reasonable assumptions need to be made during congestion, due to the shortage of congested traffic data. Section 2 introduces some traffic engineering concepts, with which bridge engineers may not be familiar.
2. Generation of a database: As the traffic Data is often not large enough to identify the rare loading events used for bridge design and assessment, an extended garage of fictitious vehicles may be generated using common Monte Carlo techniques based on the recorded data.
3. Simulation of load effects: The traffic database is passed over a bridge and the required load effects are computed, for instance using influence lines or finite element analysis; if relevant, dynamic effects are also computed.
4. Extrapolation: As it may be still quite computationally demanding to simulate traffic for very long periods, load effects are further extrapolated to find characteristic values with the safety level required by the codes of practice. These values can be then compared to the resistance of the corresponding members. Section 3 gives an overview of extreme value statistics, as it is an appropriate tool to find characteristic load effects. Sections 4 and 5 present bridge loading respectively for short and long spans, highlighting consolidated results and current research trends; emphasis is given to the combined application of traffic microsimulation and extreme value statistics to find characteristic loading values for long-span bridges.
5. Model calibration: When the target is to develop a code to be applied for a range of conditions, then a notional load model is found which envelopes the considered load effects. The calibration process often includes reliability analysis to derive appropriate partial safety factors. This step is not dealt with in this chapter; the reader can refer, for instance, to Refs. [12] or [13] for further details.
Traffic engineering concepts
The most common traffic characteristics are flow (sometimes called flux or volume), density (sometimes called concentration) and mean speed. Flow is inherently a temporal quantity (number of vehicles per unit of time), density a spatial one (number of vehicles per unit of length) and the mean speed can be either, depending on whether speed is averaged at a certain point over a time interval (time mean speed, v) or at an instant of time over a stretch of road (space mean speed, vs). Density is a key traffic variable for bridge-loading applications, as it is directly related to the number of vehicles present on a bridge at any one time. Speed is related to minimum inter-vehicle gaps: the lower the speed, the smaller the minimum safe distance between vehicles.
There are two main detector types for collecting traffic data: point detectors, which count the number of vehicles in a unit of time (the natural way to collect flow data) and spatial detectors, which count the number of vehicles in a unit of length (the natural way to collect density data). In practice, flow is far easier to measure than density, as it can be measured by means of common point detectors such as induction loops [14].
Clearly, the knowledge of vehicle positions is a prerequisite for any subsequent structural analysis. However, as traffic Data is available only at selected road cross-sections, the actual vehicle positions along a stretch of road can only be estimated from such point measurements, typically assuming constant speed. As will be shown later, this is a reasonable assumption in free-flowing traffic and therefore appropriate for short-span bridges. However, during congestion (relevant to long-span bridges), speeds may vary significantly, like in the common case of stop-and-go waves. In this case, the estimation of vehicle positions from point measurements may result in a significant loss of accuracy [15].
TRAFFIC THEORY
The Fundamental Equation of Traffic (FET) has been long used to relate flow q, density k and space mean speed vs [16, 17]:
Eq. (1) implicitly assumes that each vehicle maintains a constant speed, although individual speeds may be different. Given the large availability of point measurements, density is typically estimated from Eq. (1) from flow and speed data.1 Even when vehicles do not keep their speed, the FET might still be able to provide fairly accurate density estimates during congestion [18].
Single-vehicle data is usually aggregated over a time interval varying from 20 seconds to 5 minutes. Aggregated macroscopic variables, such as those implied in Eq. (1), are useful to obtain a global and concise description of the traffic stream. However, for bridge-loading applications, it is highly desirable to also have single-vehicle microscopic data, such as time stamps, so as to identify vehicle configurations and reconstruct vehicle positions.
The motion of individual vehicles can be fully described by tracing their trajectory, plotted over space-time domains of the traffic stream, such as in the example of Figure 1.2 Space-time domains can be generated with a rapid sequence of aerial photographs or a video [21, 22], or else with a dense installation of loop detectors or other point sensors [23]. In fact, both options are rarely practicable and currently limited to research applications.
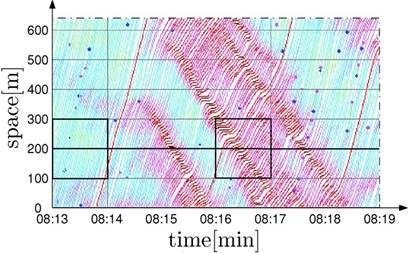
FIGURE 1.
Example of vehicle trajectories collected on the US-101 highway near Los Angeles (adapted with permission from [24]).
Let us consider the common case of a point detector. It would collect traffic data as per the straight line depicted at 200 m in Figure 1. Say the detector provides both macroscopic data aggregated every 60 s and microscopic single-vehicle data. Let us assume we are interested in inferring the density over a stretch of 100 m either sides of the point detector. In the first minute (08.13–08.14), the traffic stream flows quite steadily at about 45 km/h. Therefore, Eq. (1) applies and it is then possible to accurately infer density over the 200 m length, as well as individual vehicle positions from single-vehicle data. Afterwards, the traffic flow breaks down, developing stop-and-go waves (a stopped vehicle can be recognised when its trajectory is horizontal in the space-time domain). In the time interval 08.16–08.17, it may be possible to compute a reasonably accurate average density estimate over the 200 m length from Eq. (1), but this is likely to miss the critical maximum density occurring at some point within the 60 s aggregation time. Even when single-vehicle data is available, it is not possible to readily reconstruct the spatial distribution of vehicles, as vehicle speeds vary from those recorded when the vehicles crossed the point detector.
DATA COLLECTION
Traffic weight data is traditionally based on roadside truck surveys, or, more recently, WIM measurements. High-speed WIM stations are able to weigh axles and collect time stamps without stopping vehicles. Axle time headways can be then computed. Double loop detectors are used for supplementing information regarding speed. This enables the distance between axles to be computed and to reconstruct the vehicle configuration. The overall vehicle length can also be detected.
Data from paired WIM and loop stations has been widely used. Single-vehicle data is normally available for those stations, although sometimes only for heavy vehicles. Unfortunately, many WIM and loop detectors are not currently reliable at very low speeds [14]. As a consequence, data is largely collected during free-flowing traffic conditions, which also occur more frequently than congested conditions, whereas data about slow-moving vehicles is generally lacking.
The recorded traffic data may be directly used for subsequent structural analysis. Nevertheless, since the recorded dataset is rarely sufficiently large, it is preferable to use it as a basis to generate additional artificial traffic by means of common Monte Carlo simulations for further use in structural analysis – see for instance [25].
Except for very short spans, the next step is to reconstruct the spatial distribution of vehicles from the recorded point measurements. This is equivalent to find the headways or gaps between vehicles.3 When using individual recorded speeds, the headway h between the current vehicle i crossing the detector at a time stamp ti and the leading vehicle i-1 (that crossed the detector at a time stamp ti-1 and with speed vi-1) can be estimated as follows:
thereby assuming that the leading vehicle is keeping its speed vi-1 .4 As seen in Section 2.1, this is an acceptable assumption only in free-flowing traffic. However, when load effects are calculated during congestion, large variations in speed may result in unrealistic spatial distributions or even vehicle overlapping. This aspect is particularly significant for long spans [15].
In theory, the use of cameras over a stretch of road would provide accurate information about vehicle positions. However, there are several practical issues which make a camera-based approach difficult, such as sensitivity to lighting conditions or heavy post-processing requirements [14]. Cameras have been deployed for research purposes [21, 22, 28–30] and are becoming increasingly popular, thanks to the recent technological advances. In bridge-related studies, only a few studies report that cameras were used to collect traffic data [7, 11, 31–33].
CONGESTION
In simple terms, congestion forms whenever the inflow Qin (demand) is greater than the dynamic capacity Qout (supply). In reality, inflows greater than the dynamic capacity Qout are possible and the maximum flow that can be attained is named static capacity Qmax, or simply capacity. However, in this case, the traffic flow is not stable and a significant perturbation (e.g. a braking vehicle) could break the flow down and generate a queue (stop-and-go wave), propagating backwards at a typical speed of 15 km/h. The flow coming out of such a queue is namely the dynamic capacity or queue discharge rate. The inflow Qin can be easily collected from point detectors, whereas several procedures are available to estimate the capacity Qmax (see for instance [34]). The capacity depends on many factors, such as the road geometry; importantly for bridge-loading applications, it also depends on the truck percentage. The estimation of the dynamic capacity is not as straightforward, but research suggests it is 5–10% less than the static capacity Qmax (see for instance [35]).
Both capacities can be further reduced by bottlenecks due to a variety of causes, as will be discussed in the next section. The bottleneck strength, ΔQ, can be defined as the difference between the dynamic capacity in normal conditions, Qout, and the reduced dynamic capacity when a bottleneck is in place, Q’out:
Depending on the inflow Qin and the bottleneck strength ΔQ (and for a given traffic history), the traffic can take up any of the traffic states outlined in Table 1 [36, 37]. Combinations of congested states may also occur.
In general, increasing inflow and/or bottleneck strength has the effect of moving down the table to a higher intensity of congestion. In addition, the greater the bottleneck strength, the lower the average speed and the lower the speed oscillations during congestion [38]. Congested states that occupy a significantly long stretch of road (so-called extended states), such as SGW, OCT and HCT, are of particular significance for long-span bridge-loading applications. For comparison with the common traffic loading assumption, the full-stop condition (FS) is also included.
Spatio-temporal speed plots are useful for visualising congestion patterns (Figure 2). The space mean speed is collected at four virtual detectors and aggregated over 60 s. Figure 2(a) shows a SGW state, where the waves are clearly visible as peaks. Figure 2(b) shows a combined HCT/OCT state, where the upstream small oscillations typical of the OCT state fade away into a HCT state downstream, where there are essentially no oscillations.
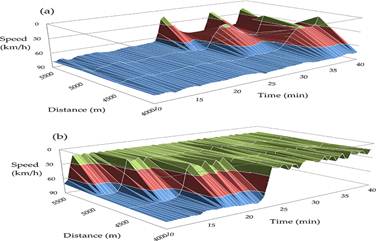
FIGURE 2.
Spatio-temporal speed plots for a simulated two-lane flow with 20% trucks and bottleneck strength: (a) 270 and (b) 1056 veh/h.
CAUSES AND EFFECTS OF CONGESTION
Congestion is due to insufficient road capacity (recurrent congestion, typically predictable and frequent) or other external causes (non-recurrent congestion, typically unpredictable and infrequent), such as inclement weather or incidents, of which incidents impact the traffic most [39, 40]. Incident rates are defined as number of incidents per million vehicle-km travelled [I/MVkmT]; therefore, the expected number of incidents strongly depends on the flow. In the context of bridge loading, the cause of an incident is not relevant; instead, its effects on the traffic capacity and subsequent congestion are relevant. For instance, the Highway Capacity Manual [34] suggests that a lane closure of a two-lane motorway drops the overall capacity by 65%. However, it must be noted that a capacity reduction does not necessarily cause congestion, as this would depend on the inflow Qin.
Table 2 presents data about incidents from selected literature. Since long-span bridges typically have two lanes in the same direction, incidents reported to cause the closure of two (or more) lanes are here considered to fully block the road; hence, the corresponding rate is named full-stop rate FSr(FS/MVkmT) [38]. Remarkably, while incident rates are spread over a wide range, full-stop rates cover a much smaller range.5
| Acronym | Traffic state |
| FT | Free Traffic |
| MLC | Moving Localised Cluster |
| PLC | Pinned Localised Cluster |
| SGW | Stop-and-Go Waves |
| OCT | Oscillating Congested Traffic |
| HCT | Homogeneous Congested Traffic |
| FS | Full Stop |
TABLE 1.
Traffic states.
TABLE 2.
Incident rates from selected literature and associated full-stop rates.
MICROSIMULATION
The concept of modelling individual vehicles, namely microsimulation, is now well established for traffic studies [24, 46, 47]. Microsimulation takes account of the interaction between vehicles, as opposed to macrosimulation, which treats traffic as an aggregate flow. As traffic microsimulation is able to reproduce realistic spatial distributions of vehicles, it is a suitable tool to investigate load effects on bridges, without resorting to conservative assumptions about heavy-vehicle positions. Notably, widely available free-flowing traffic measurements can be used to generate initial and boundary traffic conditions. Congested data may be used to calibrate and validate the microsimulation parameters [48].
Many microsimulation models have been developed in the last few decades. The choice of a suitable microsimulation model mainly relies on the traffic features of interest, e.g. during free-flowing traffic or congestion. For bridge-loading applications, the microsimulation model should be able to reproduce the range of traffic states likely to occur on a bridge. Once calibrated, microsimulation enables the modelling of a large number of congestion events (and the subsequent identification of extreme loading events), which would be extremely difficult to record in the real world.
Microsimulation models divide into car-following (single-lane) and lane-changing (multi-lane) models. While in short-span load models lane-changing manoeuvres can be neglected, they play an important role in the context of long-span bridge loading. In fact, when overtaking is allowed, the car-truck mix for congestion is likely to be different to that for free traffic, since car drivers do not feel comfortable following trucks As traffic slows down and therefore tend to overtake them [49]. This typically results in longer truck-only platoons in congested traffic than in free-flowing traffic.
THE INTELLIGENT DRIVER MODEL
The Intelligent Driver Model (IDM) is a car-following model which has been shown to successfully replicate observed multi-lane congestion patterns on several motorways With few parameters using a single-lane traffic stream made up of identical vehicles with deterministic parameters [36, 50]. The IDM has also been proven able to replicate observed single-vehicle trajectory data [51–55]. The motion of each vehicle is simulated through an acceleration function:
in which a is termed the maximum acceleration, v0 the desired speed, v(t) the current speed, s(t) the current gap to the front vehicle and s*(t) the desired minimum gap, given by:
in which s0 is termed the minimum jam (bumper-to-bumper) distance, T the safe time headway, Δv(t) the speed difference between the current vehicle and the vehicle in front and b the comfortable deceleration.6 There are five parameters in this model (v0, s0, T, a, b) to capture driver behaviour, which are relatively easy to measure. For simulation purposes, the length of the vehicles must also be known. The congested states in Table 1 can be effectively generated by applying an inhomogeneity, for instance, by increasing the safe time headway, T, downstream to – say – T‘. For a comprehensive discussion, the reader is referred to [18] or [36].
Here, it is worth mentioning that for bridge-loading applications, the parameters T and s0 greatly regulate the distance a vehicle keeps when following its leader, such that the smaller those parameters, the closer the vehicles and the Greater the loading. As speed tends to zero, the influence of the safe time headway T decreases and the spacing tends to the minimum jam distance s0. Therefore, s0 is a crucial parameter for bridge-loading applications [57].
The desired speed, v0, regulates the behaviour in free traffic, Whereas the traffic stability7 is mainly determined by a, b and T. Finally, it must be noted that the adoption of variable parameters among vehicles is not strictly necessary for reproducing the congested patterns [36, 58]. Further details about the application of the IDM to bridge-loading analysis can be found in [38].
THE MOBIL LANE-CHANGING MODEL
The MOBIL lane-changing model has been proposed in [59], to which the reader is referred For a detailed description. An overview of the model is given here, whereas details about the application of MOBIL to bridge loading can be found in [60].
Figure 3 depicts a lane change event, in which the subscript c refers to the lane-changing vehicle, orefers to the old follower (in the current lane) and n to the new one (in the target lane). All the accelerations, current and proposed (i.e. before and after the lane change), can be calculated according to the IDM given in Eqs. (4) and (5).
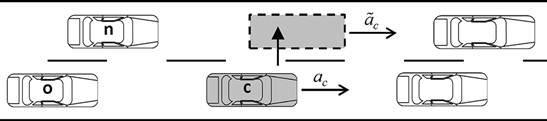
FIGURE 3.
Vehicles involved in a lane-changing manoeuvre (adapted with permission from [59]).
A lane change occurs if both incentive and safety criteria are fulfilled. For a slow-to-fast lane change, the incentive criterion is expressed as follows:

This means that the acceleration advantage ac˜−ac in performing a lane change must be greater than the sum of the acceleration threshold Δath, which prevents overtaking with a marginal advantage, the bias acceleration Δabias, which acts as an incentive to keep in the slow lane, and the imposed disadvantage to the new follower in the fast lane an−a˜n, weighted through a politeness factor p, to account for the driver aggressiveness. On the other hand, the incentive criterion for a fast-to-slow lane change is as follows:
In this case, the acceleration advantage ac˜−ac must be greater than the sum of the acceleration threshold Δath, minus the bias acceleration Δabias (which acts as an incentive to move back to the slow lane), plus the disadvantage imposed to both new follower n in the slow lane and to the current follower o in the fast lane, weighted through the politeness factor p.8
Finally, the safety criterion limits the imposed deceleration to the follower n in the target lane to the safe braking value bsafe:

SUMMARY
Traffic data for bridge-loading applications is typically collected at high-speed WIM stations. Free-flowing traffic measurements are unbiased, reliable and now commonly available. Generally speaking, if traffic information is available at a point detector, such as a WIM station, it is possible to accurately reconstruct vehicle positions from single-vehicle data only when traffic characteristics do not change significantly. This is the usual case in free-flowing traffic and therefore applicable to short-span bridges.
On the contrary, there is a shortage of data during congestion, mainly Due to current technological limitations. In addition, the analysis of traffic data can pose some issues: in fact, a vehicle’s speed is likely to fluctuate, e.g. as a result of stop-and-go waves, making the estimation of vehicle positions from point measurements problematic. The use of spatial detectors (such as cameras) over a stretch of road allows the collection of vehicle positions during congestion, without resorting to estimation. Although cameras are the best solution from a theoretical point of view, they are not often used for several practical reasons.
Traffic microsimulation provides a valuable tool for long-span bridge loading, as it is capable of reproducing realistic congested scenarios from free-flowing traffic measurements. Load effects can be computed directly from the actual spatial distribution of vehicles, thus avoiding any inaccuracy due to the estimation of vehicle positions from point measurements.
Statistics concepts
In bridge loading, extreme events with small frequencies of occurrence are of interest, rather than frequent scenarios. However, it is not generally practicable to simulate the long periods required to identify such rare events, even when the recorded database is expanded through Monte Carlo techniques. Therefore, the data is typically fitted with a statistical distribution and then extrapolated to determine characteristic loading values.
While pioneering studies focussed on wors-case scenarios [5, 6], a probabilistic approach to bridge loading is now common [7–11, 27, 33, 38, 60, 62–66]. The probability F that a load level z is not exceeded (probability of non-exceedance) is commonly expressed in terms of return period, T(z) [67]. The two variables are linked through the relation:

Importantly, the return period is different from the bridge lifetime and, instead, should be seen as a measure of safety. For instance, the characteristic and frequent values of the Load Model 1 in Eurocode 1 are based on return periods of 1000 years and 1 week, respectively [68]. The superseded British HA loading was based on a return period of 2400 years [69]. The AASHTO load model is based on 75 years [70, 71]. For assessment, it is accepted that lower return periods should be used: in Europe, a value of 75 years may be considered, whereas AASHTO [72] suggests a return period of 5 years. As will be shown in Section 5.1, such large differences in the return period do not imply equally large differences in the extrapolated characteristic values.
EXTREME VALUE STATISTICS
Extreme value theory is a branch of statistics Appropriate for the probabilistic modelling of a range of civil engineering problems. including bridge loading. A popular approach is the Block Maxima: the maximum events in each block (e.g. maximum load effect per day) are selected as representative, then fitted with a statistical distribution, and finally extrapolated to determine characteristic values. While other methods are possible, the database sample has generally more influence on the results than the extrapolation method, thus highlighting the importance of long-run simulations [73].
Firstly, an empirical frequency to each sample data point, zi (plotting position), is assigned:
in which i = 1, 2, …, N is the index of the sample ordered decreasingly.9 The Generalised Extreme Value (GEV) distribution is then fitted to the simulated maxima. Its Cumulative Distribution Function(CDF), which expresses the probability of non-exceedance F(z), is as follows [67]:
in which μ is the location, σ the scale and ξ the shape parameter. Eq. (11) is defined for any value z for which 1+ξ(z−μσ)>. When ξ = 0, the GEV distribution reduces to the Gumbel (or Type I) distribution:
When ξ > 0 and ξ < 0, the GEV distribution is named, respectively, Fréchet (or Type II) and Weibull (or Type III). The latter is more commonly found in bridge-loading applications. The GEV parameters can be inferred through maximum likelihood estimation (details can be found in [67]).
Gumbel probability paper plots are useful to illustrate the extrapolation procedure [74]. On this plot, data from a Gumbel distribution appears as a straight line. The ordinate, or Standard Extremal Variate(SEV), is given by:
Table 3 reports the target probabilities of exceedance and SEVs for typical return periods, under the common assumption that maxima are collected every day of a year with 250 working days.
THE LAW OF TOTAL PROBABILITY
The GEV distribution applies under the assumption that individual events are independent and identically distributed. However, this assumption is not necessarily met in bridge-loading applications: load effects can be the result of a number of quite different loading events, involving different numbers of trucks or different traffic states.
A generalisation of the law of total probability can be used to combine maximum load events resulting from different event types. The probability, P, that the combined maximum load effect, z, in a given reference period (e.g. a day or an hour) is not exceeded, i.e. the combined CDF, is:
![]() in which nt is the number of event types, Fj is the CDF of the maximum load effects for the j-event type (Eq. 11) and fj is the probability of occurrence of the j-event type. Clearly
in which nt is the number of event types, Fj is the CDF of the maximum load effects for the j-event type (Eq. 11) and fj is the probability of occurrence of the j-event type. Clearly
Equating P(z) to the target probability (e.g. as in Table 3) gives the characteristic combined load.
| Return period (years) | Probability of non-exceedance | SEV |
| 2400 | 0.999998 | 13.30 |
| 1000 | 0.999996 | 12.43 |
| 75 | 0.999947 | 9.84 |
| 5 | 0.999200 | 7.13 |
| 0.02 | 0.800000 | 1.50 |
TABLE 3.
Typical target probabilities of exceedance and SEV.
Eq. (14) may be applied to the combination of maximum load effects resulting from different j traffic states, each of which occurs with the assigned probability fj [38]. It implies that, within the reference period, only one maximum loading event, z, can occur due to any of the j traffic states.
On the other hand, when considering load effects deriving from different j-truck meeting events, relevant to short-span bridge loading, Eq. (14) cannot be readily applied [75]. In fact, within any reference period, there will be nt maximum loading events, each of which due to a j-truck meeting event. In this case, and only when using the GEV distribution (Eq. 11), it can be demonstrated that the probability, P, that the combined maximum load effect, z, is not exceeded in the reference period is given by [75]:
in which nt is the number of event types (typically 4) and Fj is the CDF of the GEV distribution for the maximum load effects of the j-event type.
Short-span bridges
Short-span bridges are governed by free-flowing traffic, plus an allowance for dynamic effects. Free-flowing traffic measurements can be used directly or as a basis to generate loading scenarios. The arrival of vehicles in free traffic is often idealised as a Poisson process, which can be described with a negative exponential distribution. If cars are neglected, as usually assumed in short-span bridge loading, other distributions may be more suitable to describe the arrival of truck traffic [76].
Firstly, the case of an individual lane is considered. Shorter bridge spans (< ≈30 m) are governed by a single heavy vehicle or, if very short, individual axles. Therefore, commonly available information about axle configuration and weight suffices to generate a realistic (static) load model, as there is no need to account for vehicle interaction.
For longer spans, in-lane multiple presence of heavy vehicles is a possible event. The headway between two following trucks is an important parameter to identify the number of trucks that may be simultaneously present on a bridge. Headways may be estimated from the WIM database, as discussed in Section 2.2, or from a calibrated headway model [76].
For the common case of multi-lane bridges, it is necessary to consider the multiple presence of Side-by-side heavy vehicles, whether across same-direction or opposing lanes. In the development of current European and North American codes, data about actual multiple presence of side-by-side vehicles was not collected but artificially reproduced. For instance, Reference [66] considers that one in 15 trucks has another truck side by side. This conservative assumption, used for the calibration of the current AASHTO load model [71], can be nowadays adapted to site-specific traffic conditions due to the availability of more accurate WIM data [77, 78]. Indeed, a 2-truck side-by-side meeting event is likely to strongly influence the bridge design for shorter spans (< ≈30 m) and sometimes it has also been the only considered event for longer spans [66, 79]. However, as spans get longer, the likelihood of events involving more than two trucks increases and such meeting events should be accounted for [75, 76, 80].
DYNAMIC AMPLIFICATION FACTOR
Fast-moving vehicles, typical of free-flowing traffic, interact dynamically with a bridge. The total load effect resulting from a loading event, LEt, is typically larger than would result from a static analysis, LEs. The Dynamic Amplification Factor (DAF) represents the ratio of these two load effects:
Dynamic amplification varies significantly and depends on a number of factors, such as span length, vehicle class and speed, axle spacing and weight, suspension stiffness, or the road surface profile. As described in the next section, the main codes use DAFs in the range from 1.0 to 1.8.
Reference [81] presents a review about dynamic factors for highway bridges. In recent years, the estimation of dynamic allowance has shifted from a worst-case scenario point-of-view to a probabilistic approach. In fact, several studies have identified the potential for a large DAF reduction when the static traffic loading increases, as the maximum dynamic effect does not correspond to the maximum static effect. For instance, for a single-vehicle event, there is a significant probability that a vehicle will travel at a speed which excites the bridge, whereas for a two-vehicle meeting event it is much less likely that both vehicles contribute to dynamic amplification. Moreover, a heavier vehicle typically excites the bridge less than a lighter one.
To address this issue, the Assessment Dynamic Ratio (ADR) has been proposed as the ratio between the total characteristic load effect and the static characteristic load effect [2]. These two characteristic values may not necessarily arise from the same loading scenario. Numerical investigations on dynamic vehicle-bridge interaction have found that the ADR is in the order of 1.05 [2, 82]. This considerable difference from typical dynamic allowances has the impact that many longer bridges thought to be governed by free-flowing traffic could actually be governed by congestion conditions [4]. Therefore, the simulation of congested traffic, described in Section 5.1, may have a wider application to That originally thought.
MAIN CODES
The Load Model 1 (LM1) in Eurocode 1 [68] was calibrated with 1-week WIM data collected on the A6 Motorway near Auxerre (France). The traffic scenarios were based on a dual two-lane carriageway layout. In the simulated free-flowing traffic (spans up to 50 m) a maximum of 25% trucks was considered. Nine influence lines were investigated for nine spans ranging from 5 to 200 m [64]. Several extrapolation methods were tested to find the characteristic values corresponding to the target return period of 1000 years; in general, results were not found to be very sensitive to the extrapolation technique [69]. LM1 is given as a tandem axle and a Uniformly Distributed Load (UDL), whose values depend on the lane but not on the span length. LM 1 incorporates dynamic effects: the considered DAFs were in the range 1.0 to 1.7, with the greater value for shorter span [64]. LM1 may be significantly reduced when used for site-specific bridge assessment [83].
The British code for the design of bridges [84] has been now superseded by the Eurocode. However, its main load model – The HA loading – is still prescribed for the assessment of existing highway bridges up to 50 m [85]. The HA loading is based on UK legal limits and data from roadside truck surveys [69] and consists of a UDL, given as a loading curve depending on the span length, and a Knife Edge Load (KEL). Multi-lane factors are given to consider further lanes. A DAF of 1.8 is included for single-vehicle cases . A Reduction Factor between 0.2 and 0.91 is applied to the HA design loading depending on the required assessment level, heavy traffic proportion and road surface condition .
In North America, the HL-93 model in AASHTO is based on truck surveys taken in Ontario and weigh-in-motion data. Calibration has been carried out for one- and two-lane girder bridges with single and two spans from 9 to 60 m. The model consists of a design truck, or a tandem, coincident with a design lane load. Multi-lane factors are also specified. It is specified to apply a DAF of 1.33, independent of length or load effect.
Long-span bridges
Long-span bridges are governed by congested conditions, with no allowances for dynamic effects, due to the slow speed of the vehicles involved in critical loading events. Traditionally, long-span bridge loading has been based on the simulation of queues of vehicles [5–11, 27, 63, 64]. As outlined in Section 2.4, traffic microsimulation is a powerful tool to simulate more realistic congested scenarios for long-span bridge loading.
APPLICATION OF MICROSIMULATION TO BRIDGE LOADING
An application of traffic microsimulation to long-span bridge loading is presented for a stretch of a two-lane same-direction 8000 m long highway, based on [60]. The microsimulation is carried out using the car-following IDM (Section 2.4.1) and the lane-changing model MOBIL (Section 2.4.2). In order to highlight the influence of several traffic features on bridge loading, a simplified vehicle stream made up of two classes of vehicle, cars and trucks, is used with the parameters shown in Table 4. Real sites are likely to have a more complex traffic stream, but site-specific traffic data could be equally introduced [87].
The car-following parameters are based on those calibrated and used in [36], who used only identical vehicles to successfully replicate obseved congestion patterns, as described in Section 2.4.1. Trucks are introduced here and assigned greater length and weight and slower desired speed [88, 89]. Other truck parameters are kept the same as the parameter set in [36], as consideration of different parameters is not strictly necessary to reproduce congested patterns [36, 58].
The desired speeds, v0, of both vehicle classes are uniformly randomly distributed. Although the desired speed governs the free traffic behaviour in the IDM, it is necessary to introduce speed randomness in order to correctly model lane-changing manoeuvres [59]. Trucks are assigned mean Gross Vehicle Weight (GVW) equal to the European minimum legal limit of 44 t [90, 91] and the GVW is considered normally distributed with a Coefficient of Variation (CoV: standard deviation divided by the mean) of 10%. Those two assumptions can be easily adapted to a specific site, as truck GVWs and speed histograms can be computed from WIM.
Cars and trucks are assigned the same MOBIL parameters, as calibrated in [15]. However, the assigned difference in the IDM desired speed, v0, has also the desirable effect of making trucks less prone to undertake a lane-changing manoeuvre. Notably, bridge loading is not found to be significantly sensitive to the lane-changing parameters [15].
Two long-span bridges (200 and 1000 m long) are centred at 5000 m. The dynamic capacity Qout is 3070 veh/h for a flow with 20% trucks. A range of bottleneck strengths ΔQ is generated downstream of the bridge by locally increasing the safe time headway T from 1.6 s to the values of 1.9, 2.2, 2.8, 4.0 and 6.4 s, thereby inducing the following traffic states: SGW, OCT, HCT/OCT, HCT(1) and HCT(2). HCT(1) and HCT(2) differ for the average speed of traffic (approximately 8.7 and 5.0 km/h). The full-stop condition (FS) is also simulated, for which ΔQ= Q’out.
It is assumed that congestion occurs for one hour during every working day (i.e. 250 times per year). One-year equivalent of traffic is simulated for each bottleneck strength. The hourly/daily maxima of total load are captured for subsequent statistical extrapolation with the Block Maxima approach, as described in Section 3.1. Note that load effects, such as shear or bending moment, may be equally output. However, this requires the choice of a structural form for the bridges. Since such forms may be quite different for long spans, the total load is used here to maintain generality.
IDENTIFICATION OF CRITICAL TRAFFIC STATES
The hourly maxima of total load for a flow of 3000 veh/h with 20% trucks on the two spans are plotted in Figure 4, along with the extrapolated characteristic values corresponding to return periods of 5, 75 and 1000 years.
TABLE 4.
Model parameters.
[i] – * Coefficient of variation 0.1.
In order to consider the case of the combination of congestions (Eq. 14), it is necessary to assign the congestion frequencies fj [38]. Firstly, the number of expected full-stop events, FSn is computed as follows:
in which FSr is the full-stop rate (Table 2), ADT the Average Daily Traffic (veh/day), L the length of road observed (km) and T the duration of observations (days). Here it is assumed that FSr = 0.25 FS/MVkmT [45], ADT = 32000 veh/day, T = 250 days (equivalent to one year) and L = 5 km (i.e. incidents occurring up to 5 km downstream of the bridge will affect it), thus returning 10 expected full-stop events each year. Following the previous assumption of 250 congestion events per year, this corresponds to a frequency of 4% over the total number of congestion events.
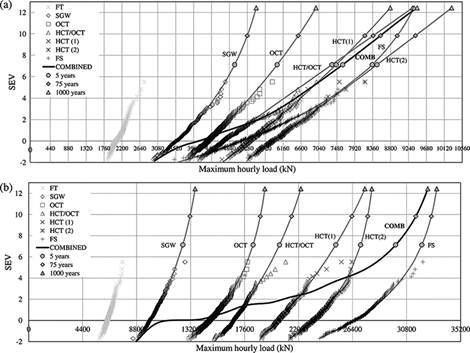
FIGURE 4.
Probability paper plots of maximum total load: (a) 200 m span; (b) 1000 m span.
The expected frequency of full-stop events is used as the basis for assigning congestion frequencies to the other bottleneck strengths generated (Figure 5). The distribution is taken to be exponential [38] and qualitatively agrees with available observations [37].
Several features can be noticed from the probability paper plots of Figure 4:
· Free traffic maxima are much lower than the congested ones.10
· Full stop is not the most critical traffic state for the 200 m span (Figure 4a) . In fact, slow-moving HCT states give more combinations of vehicles (and subsequently more chances of finding an extreme loading scenario), whereas FS is the maximum of only one realisation of vehicles, although vehicles are spaced at the minimum jam distance s0.
· For the 1000 m span (Figure 4b), FS is the most critical condition even at small return periods.
· Full-stop CDFs are characterised with a greater curvature (smaller ξ) and variability (greater σ) (Table 5).
· Oscillating congested states (SGW and OCT) do not govern the combined load, other than for small SEVs (return period less than about a week). They may actually be disregarded, as done with FT, with negligible effects on the combined characteristic load corresponding to typical return periods.11
· Separation between congested states is sharper for the 1000 m span, since local concentrations of heavy vehicles are averaged out as span increases.
· For the 200 m span (Figure 4a), considering only the most adverse congested state (HCT(2)) occurring every working day overestimates the total load by about 11% at 5 years and 9% at 1000 years, suggesting that the error in assuming only the worst congested state slightly reduces as return period increases.
· For the 1000 m span (Figure 4b), considering only the most adverse congested state (FS) occurring every working day overestimates the total load by about 7% at 5 years and 2% at 1000 years. Hence, the error in assuming only the worst congested state decreases further with increasing span.
Finally, it is noted that traffic microsimulation may be applied to free traffic as well. However, its computational requirements make this approach less attractive, compared to simpler models. Moreover, the IDM shows an excessive spreading of platoons when vehicles approach the desired speed v0 [15]. This has essentially no effect on the IDM capability of reproducing congested traffic states (as v << v0), but could potentially affect bridge loading in uncongested situations. To avoid this issue, a suitable modification of the IDM has been proposed [92].
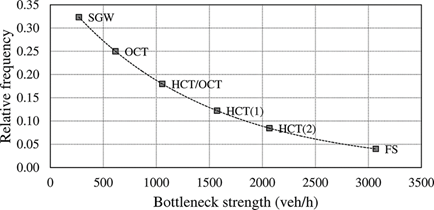
FIGURE 5.
Congestion frequencies.
TABLE 5.
Parameters of the GEV distribution for HCT and FS conditions.
INFLUENCE OF SOME TRAFFIC FEATURES
Figure 6 shows the 5-year characteristic values for the inflows of 3000 (as described in Section 5.1.1), 2000 and 1250 veh/h, expressed as an Equivalent Uniformly Distributed Load (EUDL, total load divided by bridge length). EUDLs resulting from a flow of 1250 veh/h with 48% trucks are also plotted, in order to quantify the influence of truck percentage and car presence on loading (the 1250 veh/h flow with 48% trucks has the same truck flow of the 3000 veh/h flow with 20% trucks).12
In general, the loads resulting from different inflows with same truck percentage and same bottleneck strength are quite similar (within a range of ±11%), as long as the bottleneck is strong enough to trigger congestion for that inflow, that is Qin > Q’out. This suggests that the effect of the inflow on loading is not as strong as that of bottleneck strength and implies that critical loading events may occur also out of rush hours.13
Among the traffic features affecting bridge loading, the truck percentage is of particular significance. High truck percentages may occur at night time and early morning in correspondence to low overall flows. As such, it is rare to have congestion events, but if they occur, the resulting loading is likely to be quite heavy, as there are not many cars to keep heavy vehicles apart.
Figure 6 also shows that at lower flows (1250 veh/h) FS governs for both spans and that the influence of truck percentage on the total load is expectedly large: +27.5% and +40.2% for FS, respectively, on the 200 and 1000 m span. On the other hand, the presence of cars reduces the loading by about 12% (200 m) and 29% (1000 m). Therefore, it is advised that traffic data collection should be based also on periods of low flow but with high truck percentage.
Finally, it is worth noting that the assignment of realistic congestion frequencies is certainly important for a correct bridge-loading analysis. As mentioned in Section 2.3.1, some sites are likely to be congested on a daily basis (e.g. urban corridors), whereas others can hardly experience any congestion (e.g. intercity motorways). Fortunately, the characteristic load is not largely sensitive to the congestion frequency [9, 15, 38]: it would generally suffice to consider a reasonable estimate. For instance, for the data reported above, halving the number of congestion events to 125 per year decreases the 5-year SEV to 6.44 (Eq. 13), thereby reducing the corresponding characteristic loading for the 200 m and the 1000 m respectively by 3.4% and 2.0%. If the expected congestion events are ten times less, which could make the difference between sites affected by recurrent or non-recurrent congestion, the 5-year SEV is 4.82; in this case, reductions become more significant (12.4% and 9.1%). Note that in the latter case, it is an interpolation of the simulated data that has been carried out.
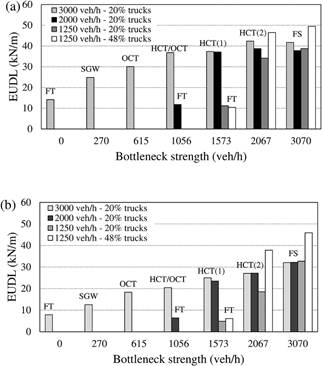
FIGURE 6.
5-year EUDL for: (a) 200 m span; (b) 1000 m span.
MAIN CODES
The calibration studies of the Eurocode LM1 considered for jammed traffic (spans 75-200 m) a queue of heavy vehicles spaced at 5 m (axle to axle) in the slow lane [64]. National Annexes may extend the span limit of application of LM1. For instance, the UK National Annex extends its application up to 1500 m. Again, LM1 may be significantly reduced when using site-specific traffic data, with traffic microsimulation used to replicate congestion events [87].
The superseded British standard [84], which specified long-span bridge loading in a similar form to the HA loading for short spans (UDL + KEL), was greatly based on [9]: truck surveys and free-flowing traffic data were used to build up queues of heavy vehicles and cars, with gaps varying from 0.9 to 1.8 m; a simple modelling of lane choice of vehicles approaching a queue was also considered.
In North America, the American Society of Civil Engineers (ASCE) recommended a load model for the design of spans up to 1951 m [93]. A UDL is to be applied in conjunction with a point load, whose values depend on span length and truck percentage. The ASCE loading is mainly based on truck data from crossings of the Second Vancouver Narrows bridge [7]. Notably, 800 full-stop events per year were considered with vehicles spaced at 1.5 m.
Summary and conclusions
In this chapter, traditional approaches and recent advances in highway bridge traffic loading are described. These are of great significance for structural safety assessment of bridges, where there is a potential for substantial savings by considering site-specific traffic conditions. An introduction to traffic theory and modelling relevant to bridge-loading applications is given, as well as an overview of extreme value statistics, since a probabilistic approach is now well established when studying bridge loading.
In bridge traffic loading, it is convenient to distinguish between short-span bridges, which are governed by free-flowing traffic plus an allowance for dynamic vehicle-bridge interaction, and long-span bridges, which are governed by congested conditions with no allowance for dynamic effects. The bridge length threshold between the two modes is not clear-cut but is thought to lie between 30 and 50 m.
Current technologies allow the collection of a great deal of traffic data during uncongested traffic conditions, mainly from weigh-in-motion stations. Such data can be used for the analysis of short-span bridges. Importantly, recent studies have shown that dynamic allowances may be significantly smaller than those considered in the main codes of practice, especially when favourable site-specific conditions are accounted for. This implies that the threshold between short- and long-span bridges may be lower than currently thought and that recent techniques to simulate congested traffic, such as those described in this chapter, may have a wider application than expected.
On the other hand, a shortage of suitable congested data has led to the fact that traffic loading on long-span bridges is often based on conservative assumptions, traditionally a queue of vehicles at minimum bumper-to-bumper distances. Traffic microsimulation is a powerful tool to generate realistic congestion patterns based on the widely available free-flowing traffic measurements. Among microsimulation models, the Intelligent Driver Model provides an optimal balance between accuracy and computational speed and can be extended with the lane-changing model MOBIL to simulate the remixing of cars and trucks occurring as traffic gets congested. Calibration of the model parameters can be based on site-specific traffic data or on available data in the literature.
Here, it is shown that microsimulation can be effectively integrated into traditional structural analysis techniques to study the effect of different traffic features on bridge loading and compute a site-specific traffic loading. Simulations on two sample spans (200 and 1000 m long) show that, besides full-stop conditions, slow-moving Homogeneous Congested Traffic (HCT) can be critical. Among several traffic features analysed, the bottleneck strength and truck percentage are found predominant. In comparison, overall traffic flow or truck traffic flow do not significantly affect total loading. Therefore, traffic data collection should also focus on periods characterised by a high truck percentage, likely to occur at night time or early morning.
In conclusion, improved computer performances are likely to make a microsimulation-based approach to highway bridge traffic loading increasingly attractive. A site-specific traffic loading can be then computed, thus allowing a more efficient planning of costly maintenance operations.



