When considering short-term prediction systems that operate in real-time and in an “intelligent” technology-based environment, the effectiveness depends, mostly, on predicting traffic information in a timely manner (Smith & Oswald, 2003). This implies that regardless of the traffic conditions met in real-time, a prediction system should not only be able to generate accurate single step ahead predictions of traffic flow, but also to operate on an iterative basis to produce reliable multiple steps ahead predictions in cases of data collection failures.

The bulk of research in short-term traffic flow prediction has concentrated on data-driven time-series models that construct the underlying rules of complex traffic datasets rather than working based on pre-determined mathematical rules; these models can be parametric – such as ARIMA models – or non-parametric (a review of the literature, methodologies and approaches used can be found in Vlahogianni et al., 2004). Among non-parametric approaches, neural networks and especially Multi-layer Feed-forward Perceptrons (MFLPs) have been shown to be most effective in forecasting traffic flow variables because of their propensity to account for a large range of traffic conditions and generate more accurate predictions than classical statistical forecasting algorithms (Smith & Oswald, 2003, Vlahogianni et al. 2004, Vlahogianni et al., 2005, Wang et al., 2006). Multi-layer Feedforward Perceptrons (MFLPs) have memoryless neurons while input activation is a function only of the current input state and not of the past input-output relations and are very popular and widely used in time series traffic forecasting partly because of their ability to capture non-linear behavior in the data structures they model, regardless of their complexity (Hornik et al., 1989). They are usually trained under a pattern-based consideration; computations aim at distinguishing clusters that have different statistical properties (mean and variance). 

However, the static operation of MLFP contradicts the temporal evolution of traffic flow. Short-term traffic flow prediction is significantly affected by the temporal evolution of traffic variables (Abdulhai et al., 2002, Stathopoulos & Karlaftis, 2003). The core research in traffic flow over the years has investigated a wide variety of nonlinear phenomena such as phase transitions (Kerner & Rehborn 1996), hysteretic effects (Hall et al. 1992, Zhang 1999), localized spatio-temporal behavior (Kerner 2002) and others. These phenomena – mainly observed in freeway bottlenecks – are difficult to predict and replicate in a simulation environment based on classical traffic flow theory (Kerner 2004). Moreover, recent efforts in

Source: Urban Transport and Hybrid Vehicles, Book edited by: Seref Soylu, 

 ISBN 978-953-307-100-8, pp. 192, September 2010, Sciyo, Croatia, downloaded from SCIYO.COM

studying the temporal evolution of traffic flow in signalized arterials have indicated that traffic volume patterns – a sequence of volume states that define the time window for prediction – exhibit significant temporal variability and demonstrated that short-term traffic flow has variable deterministic and nonlinear characteristics that can be related to the prevailing traffic flow conditions (Vlahogianni et al. 2006a, 2008). 

Although traffic flow theory has formulated improved theoretical bases in order to account for such phenomena – for example the three-phase traffic flow theory (Kerner 2004) – these effects are not taken into consideration in the process of short-term predictions using datadriven algorithms. Moreover, as indicated in most intelligent transportation system architectures, the dynamic nature of prediction algorithms are imperative to confront probable malfunctions in the data collection system or excesses in computational time (Smith & Oswald 2003, Vlahogianni et al. 2006b). 

Iterative predictions provide the means to generate information on traffic’s anticipated state with acceptable accuracy for a significant time horizon in cases of system failure. The present paper focuses on providing a comparative study between local and global iterative prediction techniques applied to traffic volume and occupancy time-series. The remainder of the paper is structured as follows: The concept of iterative predictions along with the basic notions of the proposed local and global prediction techniques in traffic flow prediction is presented in the following section. Next, the characteristics of the implementation area as well as the results of the comparative study are summarized. Finally, the paper ends with some concluding remarks.

Iterative predictions of traffic flow

Most predictions systems are dependent on data transmission. This suggests that continuous flow of volume and occupancy data is necessary to operate efficiently. However, it is common for most real-time traffic data collection systems to experience failures (Stathopoulos & Karlaftis 2003). For this, a real-time prediction system should be able to generate predictions for multiple steps ahead to ensure its operation in cases of data collection failures. The multiple steps ahead prediction problem can be formulated based on two conceptual approaches:

•       Direct approach: Given a time-series of a variable – for example volume V(t),V(t-1), …, a model is constructed to produce the state of a variable at V(t+h) steps ahead, where h >1.

•       Iterative or recursive approach: Given a time-series of a variable a single step ahead model is constructed to produce a prediction V tˆ( ) at time t that is then fed backwards to the network and is used as new input data in order to produce the next step V tˆ( + 1) prediction at t+1:

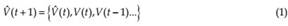
The direct approach to prediction has been implemented using neural networks in Vlahogianni et al. (2005). The reliability of direct prediction models is suspect because the model is forced to predict further ahead (Sauer 1993). This is the main argument in using iterative models in multiple steps ahead prediction. On the other hand, iterative predictions have the disadvantage of using the predicted value as input that is probably corrupted. Literature in short-term prediction of chaotic time-series indicates that the iterative approach to multiple steps ahead prediction is more accurate than direct one (Casdagli 1992).

Iterative approaches to neural network modeling have previously been applied to traffic flow predictions and results indicate that predictability decreases when the model uses previous predictions as inputs in the process of short-term predictions (Zhang 2000). This can be probably attributed to the fact that short-term traffic flow dynamics are not smooth and could not be captured by the simple structures of MLFP implemented so far (Vlahogianni et al. 2005). Two distinct categories of prediction techniques are further investigated; the local linear prediction techniques and the global neural networks. The next sub-sections provide the basics of the above techniques.

Temporal neural networks

The global iterative model to be used as an alternative theoretical approach to the proposed prediction framework is the temporal structures of neural networks. These networks are an extension of the static MLFPs that engage a memory mechanism to reconstruct the timeseries under prediction in the m-dimensional Phase Space. The memory can be limited to the input layer or can extend to the entire neural networks – for example the hidden layer – and aims at creating a State-Space reconstruction process and converts the time series data of 

The training of TLNN for iterative predictions feeds back the prediction at time t+1 and utilizes it as an input for the generation of next prediction step t +2. For global models, this simple method is plagued by the accumulation of errors and the model can quickly diverge from the desired behavior (Principe et al. 2000). For this reason the training in the specific iterative neural network model is conducted via the temporal back-propagation algorithm known as Back-propagation to time (BPTT) (Webros 1990). BPTT are trajectory learning algorithms that create virtual networks by unfolding in time the original topologies on which back-propagation training is applied; the main objective is to improve the weights so as to minimize the total error over the whole time interval (Webros 1990). More specifically, all weights are duplicated spatially for an arbitrary number of time steps τ; as such, each node that sends activation to the next has τ number of copies as well. For a training cycle n, the weight update is given by the following equation (Haykin 1999):

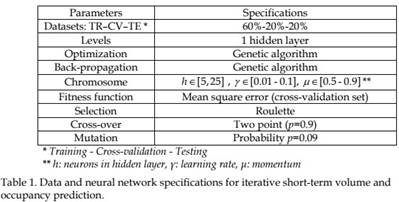
Regardless of being static or dynamic, neural networks suffer from a usually manual trialand-error process of optimization mainly with respect to their structure (number of hidden units) and learning parameters. On the other hand, automation in the optimization process of a neural network is most critical in complex neural structures. Recently, genetic algorithms have gained significant interest as they can be integrated to the neural network training to search for the optimal architecture without outside interference, thus eliminating the tedious trial and error work of manually finding an optimal network. Genetic algorithms are based on three distinct operations: selection, cross-over and mutation (Mitchell 1998); these operations run sequentially in order for a fitness criterion (in the specific case the minimization of the cross-validation error) to converge.

Implementation and results

The specific iterative prediction approach is implemented using 90-seconds volume and occupancy data collected along a signalized arterial in the centre of Athens (Greece) (Fig 1). Previous research on the area has demonstrated that traffic flow in the specific area – defined by the joint consideration of volume and occupancy – has a variable deterministic and nonlinear temporal evolution (Vlahogianni et al. 2008). The subsequent reconstruction of the series of volume and occupancy in the Phase-space using the mutual information criterion (Fraser & Swinney 1986) and the false nearest algorithm (Kennel et al. 1992) indicate that both volume and occupancy can be determined by a vector with time delay that equals to 1 and dimension that equals to 5. 

Based on the above results, the recursive prediction techniques are set to have a look-back temporal window of 1-hour to retrieve and evaluate the traffic flow patterns. Moreover, for the recursive TDNN training, the neural network is set to be unfolded in an m=5 dimensional space in order to produce predictions. The depth of the Gamma of the TLNN was also calibrated to reflect the above reconstruction. Apart from the memory mechanism,

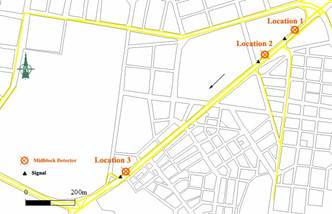
Fig. 1. Representation of the set of arterial links under study.

the difference between TDNN and TLNN implemented is that the second network extends the memory mechanism to the hidden layer too, in order to provide a fully non-stationary environment for the temporal processing of volume and occupancy series. The specifications regarding data separation as well as the genetic algorithm optimization are depicted on Table 1.

The results of the comparative study are summarized in Table 2. As can be observed the TLNN performs significantly better – with regards to the mean relative percent error of prediction – than the local weighted linear model under the iterative prediction framework in both volume and occupancy. When compared to the iterative predictions of a TDNN, it is observed that TDNN performs comparable to the TLNN. However, as the same does not apply to the case of occupancy; further statistical investigation is conducted to the series of volume and occupancy in order to explain the behavior of the models regarding occupancy predictions. Results from a simple LM ARCH (Eagle 1982) that tests the null hypothesis of no ARCH effect lying in the data series of volume and occupancy shows that occupancy exhibits higher time-varying volatility than volume that is difficult to be captured.

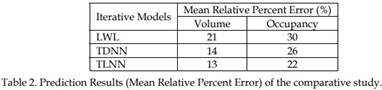
Fig 2 and Fig 3 depict the relationship of the actual and the predicted values of volume and occupancy equally. A systematic error is observed in the predictions of volume using the local prediction model. Moreover, there seems to be a difficulty in predicting high volume values as observed in Fig. 2. As for the occupancy predictions, there seem to be much more scattered that the ones of volume; R2 values are lower than the ones of volume. 

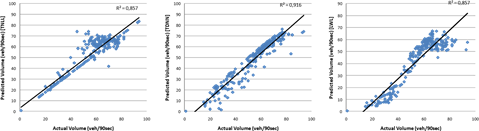
Fig. 2. Actual versus predicted values of traffic volume for the three iterative prediction techniques evaluated.

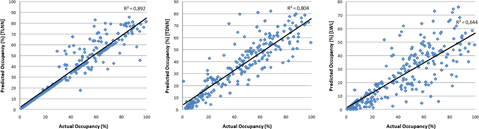
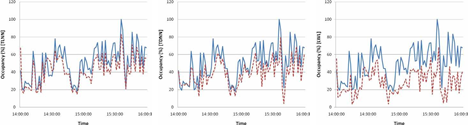
Fig. 3. Actual versus predicted values of occupancy for the three iterative prediction techniques evaluated.

In order to investigate the performance of the iterative models during the formation of congested conditions, two distinct time periods are selected for further studying the time series of the actual and predicted volume and occupancy with regards to different methodologies. These two periods depict the onset of the morning (Figure 4) and the afternoon peak (Fig. 5). 

As can be observed, although iterative TLNN exhibited improved mean relative accuracy when compared to the iterative TDNN, both models seem to capture the temporal evolution of the two traffic variables under study. In the case of afternoon peak where the series of volume exhibit a oscillating behavior – in contrast to the trend observed in volume and occupancy during the onset of the morning peak, both neural network models either overestimate of under-estimate the anticipated values of traffic volume. As for the LWL model, predictions as depicted in the time series of the actual versus the predictive values of traffic volume and occupancy can be considered as unsuccessful. 

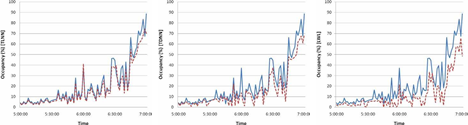
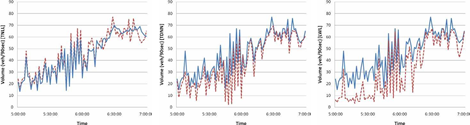
Fig. 4. Time-series of actual and predicted (dashed line) values of traffic volume (vh/90sec) for the onset of the morning peak.