Essentially, disasters are human-made. For a catastrophic event, whether precipitated by natural phenomena or human activities, assumes the state of a disaster when the community or society affected fails to cope. Earthquake hazards themselves do not necessarily lead to disasters, however intense, inevitable or unpredictable, translate to disasters only to the extent that the population is unprepared to respond, unable to deal with, and, consequently, severely affected. Seismic disasters could, in fact, be reduced if not prevented. With today’s advancements in science and technology, including early warning and forecasting of the natural phenomena, together with innovative approaches and strategies for enhancing local capacities, the impact of earthquake hazards somehow could be predicted and mitigated, its detrimental effects on populations reduced, and the communities adequately protected.
After each major earthquake, it has been concluded that the experienced ground motions were not expected and soil behavior and soil-structure interaction were not properly predicted. Failures, associated to inadequate design/construction and to lack of phenomena comprehension, obligate further code reinforcement and research. This scenario will be repeated after each earthquake. To overcome this issue, Earthquake Engineering should change its views on the present methodologies and techniques toward more scientific, doable, affordable, robust and adaptable solutions.
A competent modeling of engineering systems, when they are affected by seismic activity, poses many difficult challenges. Any representation designed for reasoning about models of such systems has to be flexible enough to handle various degrees of complexity and uncertainty, and at the same time be sufficiently powerful to deal with situations in which the input signal may or may not be controllable.Mathematically-based models are developed using scientific theories and concepts that just apply to particular conditions. Thus, the core of the model comes from assumptions that for complex systems usually lead to simplifications (perhaps oversimplifications) of the problem phenomena. It is fair to argue that the representativeness of a particular theoretical model largely depends on the degree of comprehension the developer has on the behavior of the actual engineering problem. Predicting natural-phenomena characteristics like those of earthquakes, and thereupon their potential effects at particular sites, certainly belong to a class of problems we do not fully understand. Accordingly, analytical modeling often becomes the bottleneck in the development of more accurate procedures. As a consequence, a strong demand for advanced modeling an identification schemes arises.
Cognitive Computing CC technologies have provided us with a unique opportunity to establish coherent seismic analysis environments in which uncertainty and partial data-knowledge are systematically handled. By seamlessly combining learning, adaptation, evolution, and fuzziness, CC complements current engineering approaches allowing us develop a more comprehensive and unified framework to the effective management of earthquake phenomena. Each CC algorithm has well-defined labels and could usually be identified with specific scientific communities. Lately, as we improved our understanding of these algorithms’ strengths and weaknesses, we began to leverage their best features and developed hybrid algorithms that indicate a new trend of co-existence and integration between many scientific communities to solve a specific task.
In this chapter geotechnical aspects of earthquake engineering under a cognitive examination are covered. Geotechnical earthquake engineering, an area that deals with the design and construction of projects in order to resist the effect of earthquakes, requires an understanding of geology, seismology and earthquake engineering. Furthermore, practice of geotechnical earthquake engineering also requires consideration of social, economic and political factors. Via the development of cognitive interpretations of selected topics: i) spatial variation of soil dynamic properties, ii) attenuation laws for rock sites (seismic input), iii) generation of artificial-motion time histories, iv) effects of local site conditions (site effects), and iv) evaluation of liquefaction susceptibility, CC techniques (Neural Networks NNs, Fuzzy Logic FL and Genetic Algorithms GAs) are presented as appealing alternatives for integrated data-driven and theoretical procedures to generate reliable seismic models.
Geotechnical earthquake hazards
The author is well aware that standards for geotechnical seismic design are under development worldwide. While there is no need to “reinvent the wheel” there is a requirement to adapt such initiatives to fit the emerging safety philosophy and demands. This investigation also strongly endorses the view that “guidelines” are far more desirable than “codes” or “standards” disseminated all over seismic regions. Flexibility in approach is a key ingredient of geotechnical engineering and the cognitive technology in this area is rapidly advancing.The science and practice of geotechnical earthquake engineering is far from mature and need to be expanded and revised periodically in coming years. It is important that readers and users of the computational models presented here familiarize themselves with the latest advances and amend the recommendations herein appropriately.
This document is not intended to be a detailed treatise of latest research in geotechnical earthquake engineering, but to provide sound guidelines to support rational cognitive approaches. While every effort has been made to make the material useful in a wider range of applications, applicability of the material is a matter for the user to judge. The main aim of this guidance document is to promote consistency of cognitive approach to everyday situations and, thus, improve geotechnical-earthquake aspects of the performance of the built safe-environment.
A “SOFT” INTERPRETATION OF GROUND MOTIONS
After a sudden rupture of the earth’s crust (caused by accumulating stresses, elastic strain-energy) a certain amount of energy radiates from the rupture as seismic waves. These waves are attenuated, refracted, and reflected as they travel through the earth, eventually reaching the surface where they cause ground shaking. The principal geotechnical hazards associated with this event are fault rupture, ground shaking, liquefaction and lateral spreading, and landsliding. Ground shaking is one of the principal seismic hazards that causes extensive damage to the built environment and failure of engineering systems over large areas. Earthquake loads and their effects on structures are directly related to the intensity and duration of ground shaking. Similarly, the level of ground deformation, damage to earth structures and ground failures are closely related to the severity of ground shaking.
In engineering evaluations, three characteristics of ground shaking are typically considered: i) the amplitude, ii) frequency content and iii) significant duration of shaking (time over which the ground motion has relatively significant amplitudes).These characteristics of the ground motion at a given site are affected by numerous complex factors such as the source mechanism, earthquake magnitude, rupture directivity, propagation path of seismic waves, source distance and effects of local soil conditions. There are many unknowns and uncertainties associated with these issues which in turn result in significant uncertainties regarding the characteristics of the ground motion and earthquake loads.
If the random nature of response to earthquakes (aleatory uncertainty) cannot be avoided [1,2], it is our limited knowledge about the patterns between seismic events and their manifestations -ground motions- at a site (epistemic uncertainty) that must be improved thorough more scientific seismic analyses. A strategic factor in seismic hazard analysis is the ground motion model or attenuation relation. These attenuation relationships has been developed based on magnitude, distance and site category, however, there is a tendency to incorporate other parameters, which are now known to be significant, as the tectonic environment, style of faulting and the effects of topography, deep basin edges and rupture directivity. These distinctions are recognized in North America, Japan and New Zealand [3-6], but ignored in most other regions of the world [7]. Despite recorded data suggest that ground motions depend, in a significant way, on these aspects, these inclusions did not have had a remarkable effect on the predictions confidence and the geotechnical earthquake engineer prefers the basic and clear-cut approximations on those that demand a blind use of coefficients or an intricate determination of soil/fault conditions.
A key practice in current aseismic design is to develop design spectrum compatible time histories. This development entails the modification of a time history so that its response spectrum matches within a prescribed tolerance level, the target design spectrum. In such matching it is important to retain the phase characteristics of the selected ground motion time history. Many of the techniques used to develop compatible motions do not retain the phase [8]. The response spectrum alone does not adequately characterize specific-fault ground motion. Near-fault ground motions must be characterized by a long period pulse of strong motion of a fairly brief duration rather than the stochastic process of long duration that characterizes more distant ground motions. Spectrum compatible with these specific motions will not have these characteristics unless the basic motion being modified to ensure compatibility has these effects included. Spectral compatible motions could match the entire spectrum but the problem arises on finding a “real” earthquake time series that match the specific nature of ground motion. For nonlinear analysis of structures, spectrum compatible motions should also correspond to the particular energy input [9], for this reason, designers should be cautious about using spectrum compatible motions when estimating the displacements of embankment dams and earth structures under strong shaking, if the acceptable performance of these structures is specified by criteria based on tolerable displacements.
Another important seismic phenomenon is the liquefaction. Liquefaction is associated with significant loss of stiffness and strength in the shaken soil and consequent large ground deformation. Particularly damaging for engineering structures are cyclic ground movements during the period of shaking and excessive residual deformations such as settlements of the ground and lateral spreads. Ground surface disruption including surface cracking, dislocation, ground distortion, slumping and permanent deformations, large settlements and lateral spreads are commonly observed at liquefied sites. In sloping ground and backfills behind retaining structures in waterfront areas, liquefaction often results in large permanent ground displacements in the down-slope direction or towards waterways (lateral spreads). Dams, embankments and sloping ground near riverbanks where certain shear strength is required for stability under gravity loads are particularly prone to such failures. Clay soils may also suffer some loss of strength during shaking but are not subject to boils and other “classic” liquefaction phenomena. For intermediate soils, the transition from “sand like” to “clay-like” behavior depends primarily on whether the soil is a matrix of coarse grains with fines contained within the pores or a matrix of plastic fines with coarse grained “filler”. Recent papers by Boulanger and Idriss [10, 11] are helpful in clarifying issues surrounding the liquefaction and strain softening of different soil types during strong ground shaking. Engineering judgment based on good quality investigations and data interpretation should be used for classifying such soils as liquefiable or non-liquefiable.
Procedures for evaluating liquefaction, potential and induced lateral spread, have been studied by many engineering committees around the world. The objective has been to review research and field experience on liquefaction and recommended standards for practice. Youd and Idriss [12] findings and the liquefaction-resistance chart proposed by Seed et al. [13] in 1985, stay as standards for practice. They have been slightly modified to adjust new registered input-output conditions and there is a strong tendency to recommend i) the adoption of the cone penetration test CPT, standard penetration test SPT or the shear wave velocities for describing the in situ soil conditions [14] and ii) the modification of magnitude factors used to convert the critical stress ratios from the liquefaction assessment charts (usually developed for M7:5) to those appropriate for earthquakes of diverse magnitudes [12, 15].
Cognitive Computing
Cognitive Computing CC as a discipline in a narrow sense, is an application of computers to solve a given computational problem by imperative instructions; while in a broad sense, it is a process to implement the instructive intelligence by a system that transfers a set of given information or instructions into expected behaviors. According to theories of cognitive informatics [16-18], computing technologies and systems may be classified into the categories of imperative, autonomic, and cognitive from the bottom up. Imperative computing is a traditional and passive technology based on stored-program controlled behaviors for data processing [19-24]. An autonomic computing is goal-driven and self-decision-driven technologies that do not rely on instructive and procedural information [25-28]. Cognitive computing is more intelligent technologies beyond imperative and autonomic computing, which embodies major natural intelligence behaviors of the brain such as thinking, inference, learning, and perceptions.
Cognitive computing is an emerging paradigm of intelligent computing methodologies and systems, which implements computational intelligence by autonomous inferences and perceptions mimicking the mechanisms of the brain. This section presents a brief description on the theoretical framework and architectural techniques of cognitive computing beyond conventional imperative and autonomic computing technologies. Cognitive models are explored on the basis of the latest advances in applying computational intelligence. These applications of cognitive computing are described from the aspects of cognitive search engines, which demonstrate how machine and computational intelligence technologies can drive us toward autonomous knowledge processing.
COMPUTATIONAL INTELLIGENCE: SOFT COMPUTING TECHNOLOGIES
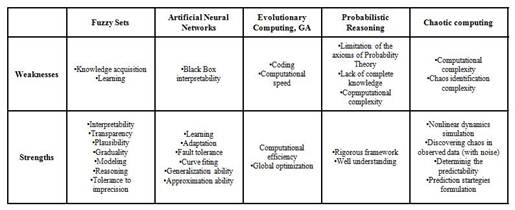
The computational intelligence is a synergistic integration of essentially three computing paradigms, viz. neural networks, fuzzy logic and evolutionary computation entailing probabilistic reasoning (belief networks, genetic algorithms and chaotic systems) [29]. This synergism provides a framework for flexible information processing applications designed to operate in the real world and is commonly called Soft Computing SC [30]. Soft computing technologies are robust by design, and operate by trading off precision for tractability. Since they can handle uncertainty with ease, they conform better to real world situations and provide lower cost solutions.
The three components of soft computing differ from one another in more than one way. Neural networks operate in a numeric framework, and are well known for their learning and generalization capabilities. Fuzzy systems [31] operate in a linguistic framework, and their strength lies in their capability to handle linguistic information and perform approximate reasoning. The evolutionary computation techniques provide powerful search and optimization methodologies. All the three facets of soft computing differ from one another in their time scales of operation and in the extent to which they embed a priori knowledge.
Figure 1 shows a general structure of Soft Computing technology. The following main components of SC are known by now: fuzzy logic FL, neural networks NN, probabilistic reasoning PR, genetic algorithms GA, and chaos theory ChT (Figure 1). In SC FL is mainly concerned with imprecision and approximate reasoning, NN with learning, PR with uncertainty and propagation of belief, GA with global optimization and search and ChT with nonlinear dynamics. Each of these computational paradigms (emerging reasoning technologies) provides us with complementary reasoning and searching methods to solve complex, real-world problems. In large scope, FL, NN, PR, and GA are complementary rather that competitive [32-34]. The interrelations between the components of SC, shown in Figure 1, make the theoretical foundation of Hybrid Intelligent Systems. As noted by L. Zadeh: “… the term hybrid intelligent systems is gaining currency as a descriptor of systems in which FL, NC, and PR are used in combination. In my view, hybrid intelligent systems are the wave of the future” [35]. The use of Hybrid Intelligent Systems are leading to the development of numerous manufacturing system, multimedia system, intelligent robots, trading systems, which exhibits a high level of MIQ (machine intelligence quotient).
COMPARATIVE CHARACTERISTICS OF SC TOOLS
The constituents of SC can be used independently (fuzzy computing, neural computing, evolutionary computing etc.), and more often in combination [36, 37, 38- 40, 41]. Based on independent use of the constituents of Soft Computing, fuzzy technology, neural technology, chaos technology and others have been recently applied as emerging technologies to both industrial and non-industrial areas.
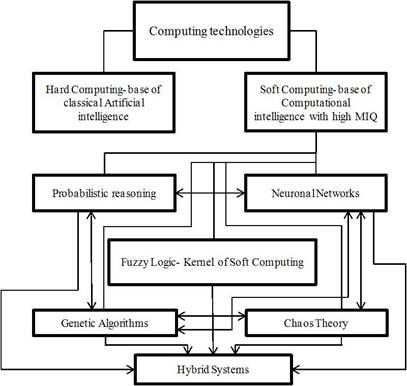
FIGURE 1.
Soft Computing Components
Fuzzy logic is the leading constituent of Soft Computing. In Soft Computing, fuzzy logic plays a unique role. FL serves to provide a methodology for computing [36]. It has been successfully applied to many industrial spheres, robotics, complex decision making and diagnosis, data compression, and many other areas. To design a system processor for handling knowledge represented in a linguistic or uncertain numerical form we need a fuzzy model of the system. Fuzzy sets can be used as a universal approximator, which is very important for modeling unknown objects. If an operator cannot tell linguistically what kind of action he or she takes in a specific situation, then it is quite useful to model his/her control actions using numerical data. However, fuzzy logic in its so called pure form is not always useful for easily constructing intelligent systems. For example, when a designer does not have sufficient prior information (knowledge) about the system, development of acceptable fuzzy rule base becomes impossible. As the complexity of the system increases, it becomes difficult to specify a correct set of rules and membership functions for describing adequately the behavior of the system. Fuzzy systems also have the disadvantage of not being able to extract additional knowledge from the experience and correcting the fuzzy rules for improving the performance of the system.
Another important component of Soft Computing is neural networks. Neural networks NN viewed as parallel computational models, are parallel fine-grained implementation of non-linear static or dynamic systems. A very important feature of these networks is their adaptive nature, where “learning by example” replaces traditional “programming” in problems solving. Another key feature is the intrinsic parallelism that allows fast computations. Neural networks are viable computational models for a wide variety of problems including pattern classification, speech synthesis and recognition, curve fitting, approximation capability, image data compression, associative memory, and modeling and control of non-linear unknown systems [42, 43]. NN are favorably distinguished for efficiency of their computations and hardware implementations. Another advantage of NN is generalization ability, which is the ability to classify correctly new patterns. A significant disadvantage of NN is their poor interpretability. One of the main criticisms addressed to neural networks concerns their black box nature [35].
Evolutionary Computing EC is a revolutionary approach to optimization. One part of EC—genetic algorithms—are algorithms for global optimization. Genetic algorithms GAs are based on the mechanisms of natural selection and genetics [44]. One advantage of genetic algorithms is that they effectively implement parallel multi-criteria search. The mechanism of genetic algorithms is simple. Simplicity of operations and powerful computational effect are the two main advantages of genetic algorithms. The disadvantages are the problem of convergence and the absence of strong theoretical foundation. The requirement of coding the domain of the real variables’ into bit strings also seems to be a drawback of genetic algorithms. It should be also noted that the computational speed of genetic algorithms is low.
Because in this investigation PR and ChT are not exploited, they are not going to be explained. For the interested reader [41] is recommended. Table 1 presents the comparative characteristics of the components of Soft Computing. For each component of Soft Computing there is a specific class of problems, where the use of other components is inadequate.
INTELLIGENT COMBINATIONS OF SC
As it was shown above, the components of SC complement each other, rather than compete. It becomes clear that FL, NC and GA are more effective when used in combinations. Lack of interpretability of neural networks and poor learning capability of fuzzy systems are similar problems that limit the application of these tools. Neurofuzzy systems are hybrid systems which try to solve this problem by combining the learning capability of connectionist models with the interpretability property of fuzzy systems. As it was noted above, in case of dynamic work environment, the automatic knowledge base correction in fuzzy systems becomes necessary. On the other hand, artificial neural networks are successfully used in problems connected to knowledge acquisition using learning by examples with the required degree of precision.
Incorporating neural networks in fuzzy systems for fuzzification, construction of fuzzy rules, optimization and adaptation of fuzzy knowledge base and implementation of fuzzy reasoning is the essence of the Neurofuzzy approach.
TABLE 1.
Central characteristics of Soft Computing technologies
The combination of genetic algorithms with neural networks yields promising results as well. It is known that one of main problems in development of artificial neural systems is selection of a suitable learning method for tuning the parameters of a neural network (weights, thresholds, and structure). The most known algorithm is the “error back propagation” algorithm. Unfortunately, there are some difficulties with “back propagation”. First, the effectiveness of the learning considerably depends on initial set of weights, which are generated randomly. Second, the “back propagation”, like any other gradient-based method, does not avoid local minima. Third, if the learning rate is too slow, it requires too much time to find the solution. If, on the other hand, the learning rate is too high it can generate oscillations around the desired point in the weight space. Fourth, “back propagation” requires the activation functions to be differentiable. This condition does not hold for many types of neural networks. Genetic algorithms used for solving many optimization problems when the “strong” methods fail to find appropriate solution, can be successfully applied for learning neural networks, because they are free of the above drawbacks.
The models of artificial neurons, which use linear, threshold, sigmoidal and other transfer functions, are effective for neural computing. However, it should be noted that such models are very simplified. For example, reaction of a biological axon is chaotic even if the input is periodical. In this aspect the more adequate model of neurons seems to be chaotic. Model of a chaotic neuron can be used as an element of chaotic neural networks. The more adequate results can be obtained if using fuzzy chaotic neural networks, which are closer to biological computation. Fuzzy systems with If-Then rules can model non-linear dynamic systems and capture chaotic attractors easily and accurately. Combination of Fuzzy Logic and Chaos Theory gives us useful tool for building system’s chaotic behavior into rule structure. Identification of chaos allows us to determine predicting strategies. If we use a Neural Network Predictor for predicting the system’s behavior, the parameters of the strange attractor (in particular fractal dimension) tell us how much data are necessary to train the neural network. The combination of Neurocomputing and Chaotic computing technologies can be very helpful for prediction and control.
The cooperation between these formalisms gives a useful tool for modeling and reasoning under uncertainty in complicated real-world problems. Such cooperation is of particular importance for constructing perception-based intelligent information systems. We hope that the mentioned intelligent combinations will develop further, and the new ones will be proposed. These SC paradigms will form the basis for creation and development of Computational Intelligence.
Cognitive models of ground motions
The existence of numerous databases in the field of civil engineering, and in particular in the field of geotechnical earthquake, has opened new research lines through the introduction of analysis based on soft computing. Three methods are mainly applied in this emerging field: the ones based on the Neural Networks NN, the ones created using Fuzzy Sets FS theory and the ones developed from the Evolutionary Computation [45].
The SC hybrids used in this investigation are directed to tasks of prediction (classification and/or regression). The central objective is obtaining numerical and/or categorical values that mimic input-output conditions from experimentation and in situ measurements and then, through the recorded data and accumulated experience, predict future behaviors. The examples presented herein have been developed by an engineering committee that works for generating useful guidance to geotechnical practitioners with geotechnical seismic design. This effort could help to minimize the perceived significant and undesirable variability within geotechnical earthquake practice. Some urgency in producing the alternative guidelines was seen, after the most recent earthquakes disasters, as being necessary with a desire to avoid a long and protracted process. To this end, a two stage approach was suggested with the first stage being a cognitive interpretation of well-known procedures with appropriate factors for geotechnical design, and a posterior step identifying the relevant philosophy for a new geotechnical seismic design.
SPATIAL VARIATION OF SOIL DYNAMIC PROPERTIES
The spatial variability of subsoil properties constitutes a major challenge in both the design and construction phases of most geo-engineering projects. Subsoil investigation is an imperative step in any civil engineering project. The purpose of an exploratory investigation is to infer accurate information about actual soil and rock conditions at the site. Soil exploration, testing, evaluation, and field observation are well-established and routine procedures that, if carried out conscientiously, will invariably lead to good engineering design and construction. It is impossible to determine the optimum spacing of borings before an investigation begins because the spacing depends not only on type of structure but also on uniformity or regularity of encountered soil deposits. Even the most detail soil maps are not efficient enough for predicting a specific soil property because it changes from place to place, even for the same soil type. Consequently interpolation techniques have been extensively exploited. The most commonly used methods are kriging and co-kriging but for better estimations they require a great number of measurements available for each soil type, what is generally impossible.
Based on the high cost of collecting soil attribute data at many locations across landscape, new interpolation methods must be tested in order to improve the estimation of soil properties. The integration of GIS and Soft Computing SC offers a potential mechanism to lower the cost of analysis of geotechnical information by reducing the amount of time spent understanding data. Applying GIS to large sites, where historical data can be organized to develop multiple databases for analytical and stratigraphic interpretation, originates the establishment of spatial/chronological efficient methodologies for interpreting properties (soil exploration) and behaviors (in situ measured). GIS-SC modeling/simulation of natural systems represents a new methodology for building predictive models, in this investigation NN and GAs, nonparametric cognitive methods, are used to analyze physical, mechanical and geometrical parameters in a geographical context. This kind of spatial analysis can handle uncertain, vague and incomplete/redundant data when modeling intricate relationships between multiple variables. This means that a NN has not constraints about the spacing (minimum distance) between the drill holes used for building (training) the SC model. The NNs-GAs acts as computerized architectures that can approximate nonlinear functions of several variables, this scheme represent the relations between the spatial patterns of the stratigraphy without restrictive assumptions or excessive geometrical and physical simplifications.
The geotechnical data requirements (geo-referenced properties) for an easy integration of the SC technologies are explained through an application example: a geo-referenced three-dimensional model of the soils underlying Mexico City. The classification/prediction criterion for this very complex urban area is established according to two variables: the cone penetration resistance qc (mechanical property) and the shear wave velocity Vs (dynamic property). The expected result is a 3D-model of the soils underlying the city area that would eventually be improved for a more complex and comprehensive model adding others mechanical, physical or geometrical geo-referenced parameters.
Cone-tip penetration resistances and shear wave velocities have been measured along 16 bore holes spreaded throughout the clay deposits of Mexico City (Figure 2). This information was used as the set of examples inputs (latitude, longitude and depth) → output (qc /Vs). The analysis was carried out in an approximate area of 125 km2 of Mexico City downtown. It is important to point out that 20% of these patterns (sample points and complete variables information) are not used in the training stage; they will be presented for testing the generalization capabilities of the closed system components (once the training is stopped).
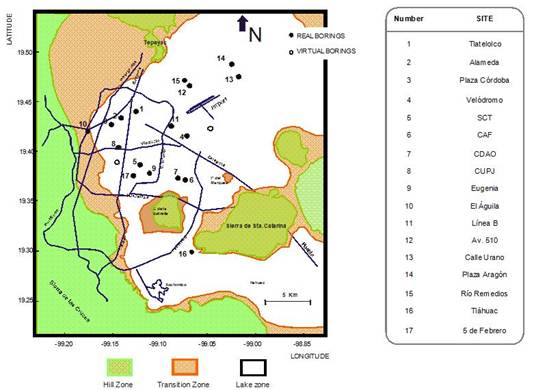
FIGURE 2.
Mexico City Zonation
In the 3D-neurogenetic analysis, the functions qc={qc(X,Y,Z)}/Vs={Vs(X,Y,Z)} are to be approximated using the procedure outlined below:
1. Generate the database including identification of the site [borings or stations] (X,Y –geographical coordinates, Z –depth, and a CODE –ID number), elevation reference (meters above de sea level, m.a.s.l.), thickness of predetermined structures (layers), and additional information related to geotechnical zoning that could be useful for results interpretation.
2. Use the database to train an initial neural topology whose weights and layers are tuned by an evolutive algorithm (see [46] for details), until the minimum error between calculated and measured values qc=fNN(X,Y,Z)}/Vs={fNN(X,Y,Z)} is achieved (Figure 3a). The generalization capabilities of the optimal 3D neural model are tested presenting real work cases (information from borings not included in the training set) to the net. Figure 3b presents the comparison between the measuredqcqc, Vsvalues and the NN calculations for testing cases. Through the neurogenetic results for unseen situations we can conclude that the procedure works extremely well in identifying the general trend in materials resistance (stiffness). The correlation between NN calculations and “real” values is over 0.9.
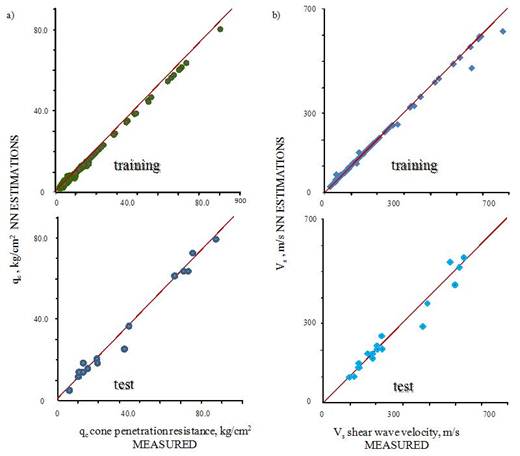
FIGURE 3.
Neural estimations of mechanical and dynamic parameters
1. For visual environment requirements a grid is constructed using raw information and neurogenetic estimations for defining the spatial variation of properties (Figure 4). The 3D view of the studied zone represents an easier and more understandable engineering system. The 3D neurogenetic-database also permits to display property-contour lines for specific depths. Using the neurogenetic contour maps, the spatial distribution of the mechanical/dynamic variables can be visually appreciated. The 3D model is able to reflect the stratigraphical patterns (Figure 5), indicating that the proposed networks are effective in site characterization with remarkable advantages if comparing with geostatistical approximations: it is easier to use, to understand and to develop graphical user interfaces. The confidence and practical advantages of the defined neurogenetic layers is evident. Precision of predictions depends on neighborhood structure, grid size, and variance response, but based on the results we can conclude that despite of the grid cell (size) is not too small the spatial correlation extends beyond the training neighborhood, but the higher confidence is obviously only within.
2.
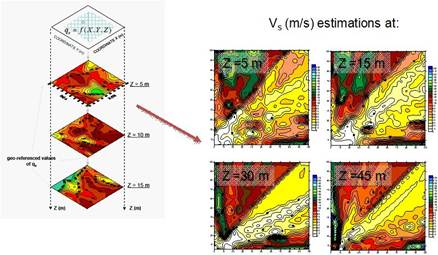
FIGURE 4.
Neural response
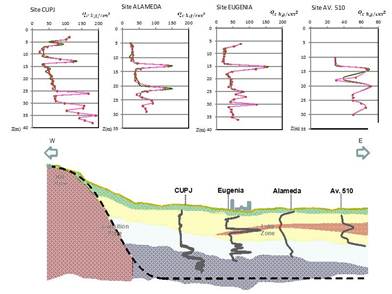
FIGURE 5.
Stratigraphy sequence obtained using the 3D Neural estimations
ATTENUATION LAWS FOR ROCK SITE (OUTCROPPING MOTIONS)
Source, path, and local site response are factors that should be considered in seismic hazard analyses when using attenuation relations. These relations, obtained from statistical regression, are derived from strong motion recordings to define the occurrence of an earthquake with a specific magnitude at a particular distance from the site. Because of the uncertainties inherent in the variables describing the source (e.g. magnitude, epicentral distance, focal depth and fault rupture dimension), the difficulty to define broad categories to classify the site (e.g. rock or soil) and our lack of understanding regarding wave propagation processes and the ray path characteristics from source to site, commonly the predictions from attenuation regression analyses are inaccurate. As an effort to recognize these aspects, multiparametric attenuation relations have been proposed by several researchers [47-53]. However, most of these authors have concluded that the governing parameters are still source, ray path, and site conditions. In this section an empirical NN formulation that uses the minimal information about magnitude, epicentral distance, and focal depth for subduction-zone earthquakes is developed to predict the peak ground acceleration PGA and spectral accelerations SaSa at a rock-like site in Mexico City.
The NN model was training from existing information compiled in the Mexican strong motion database. The NN uses earthquake moment magnitudeMwMw, epicentral distanceEDED, and focal depth FDFD from hundreds of events recorded during Mexican subduction earthquakes (Figure 6) from 1964 to 2007. To test the predicting capabilities of the neuronal model, 186 records were excluded from the data set used in the learning phase. Epicentral distance EDED is considered to be the length from the point where fault-rupture starts to the recording site, and the focal depth FDFD is not declared as mechanism classes, the NN should identify the event type through the FDFD crisp value coupled with the others input parameters [54, 47, 55], The interval of MwMw goes from 3 to 8.1 approximately and the events were recorded at near (a few km) and far field stations (about 690 km). The depth of the zone of energy release ranged from very shallow to about 360 km.
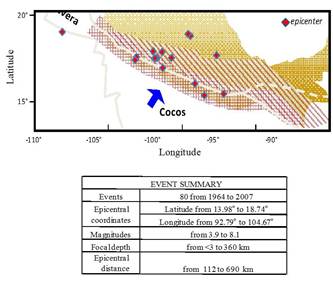
FIGURE 6.
Earthquakes characteristics
Modeling of the data base has been performed using backpropagation learning algorithm. Horizontal (mutually orthogonalPGAh1PGAh1, N-S component, andPGAh2PGAh2, E-W component) and vertical components (PGAvPGAv) are included as outputs for neural mapping. After trying many topologies, the best horizontal and vertical modules with quite acceptable approximations were the simpler alternatives (BP backpropagation, 2 hidden layers/15 units or nodes each). The neuronal attenuation model for {Mw,ED,FD}→{PGAh1,PGAh2,PGAv}{Mw,ED,FD}→{PGAh1,PGAh2,PGAv} was evaluated by performing testing analyses. The predictive capabilities of the NNs were verified by comparing the estimated PGA’s to those induced by the 186 events excluded from the original database (data for training stage). In Figure 7 are compared the computed PGA’s during training and testing stages to the measured values. The relative correlation factors (R2≆0.97R2≇0.97), obtained in the training phase, indicate that those topologies selected as optimal behave consistently within the full range of intensity, distances and focal depths depicted by the patterns. Once the networks converge to the selected stop criterion, learning is finished and each of these black-boxes become a nonlinear multidimensional functional. Following this procedure 20 NN are trained to evaluate de SaSa at different response spectra periods (from T= 0.1 s to T= 5.0 s with DT=0.25 s). Forecasting of the spectral components is reliable enough for practical applications.

FIGURE 7.
Some examples of measured and NN-estimated PGA values
In Figure 8 two case histories correspond to large and medium size events are shown, the estimated values obtained for these events using the relationships proposed by Gómez, Ordaz &Tena [56], Youngs et al. [47], Atkinson and Boore [55] –proposed for rock sites– and Crouse et al. [51] –proposed for stiff soil sites– and the predictions obtained with the PGAh1−h2PGAh1-h2modules are shown. It can be seen that the estimation obtained with Gómez, Ordaz y Tena [56] seems to underestimate the response for the large magnitude event. However, for the lower magnitude event follows closely both the measured responses and NN predictions. Youngs et al. [47] attenuation relationship follows closely the overall trend but tends to fall sharply for long epicentral distances.
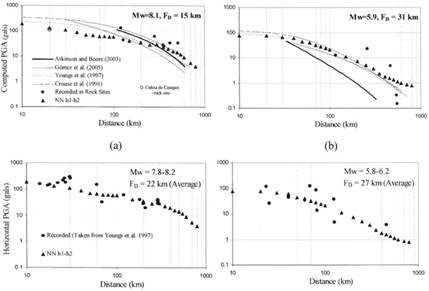
FIGURE 8.
Attenuation laws comparisons
Furthermore, it should be stressed the fact that, as can be seen in Figure 9 the neural attenuation model is capable to follow the general behavior of the measure data expressed as spectra while the traditional functional approaches are not able to reproduce. A neural sensitivity study for the input variables was conducted for the neuronal modules. The results are strictly valid only for the data base utilized, nevertheless, after several sensitivity analyses conducted changing the database composition, it was found that the following trend prevails; theMwMw would be the most relevant parameter then would follow EDED coupled with FDFD. However, for near site events the epicentral distance could become as relevant as the magnitude, particularly, for the vertical component and for minor earthquakes (M low) the FDFD becomes very transcendental.
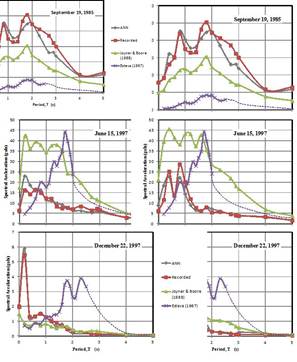
FIGURE 9.
Response Spectra: NN-calculated vs traditional functions
Through{Mw,ED,FD}→{PGAhi,Sa}{Mw,ED,FD}→{PGAhi,Sa} mapping, this neuronal approach offers the flexibility to fit arbitrarily complex trends in magnitude and distance dependence and to recognize and select among the tradeoffs that are present in fitting the observed parameters within the range of magnitudes and distances present in data. This approach seems to be a promising alternative to describe earthquake phenomena despite of the limited observations and qualitative knowledge of the recording stations geotechnical site conditions, which leads to a reasoning of a partially defined behavior.
GENERATION OF ARTIFICIAL TIME SERIES: ACCELEROGRAMS APPLICATION
For nonlinear seismic response analysis, where the superposition techniques do not apply, earthquake acceleration time histories are required as inputs. Virtually all seismic design codes and guidelines require scaling of selected ground motion time histories so that they match or exceed the controlling design spectrum within a period range of interest. Considerable variability in the characteristics of the recorded strong-motions under similar conditions may still require a characterization of future shaking in terms of an ensemble of accelerograms rather than in terms of just one or two “typical” records. This situation has thus created a need for the generation of synthetic (artificial) strong-motion time histories that simulate realistic ground motions from different points of views and/or with different degrees of sophistication. To provide the ground motions for analysis and design, various methods have been developed: i) frequency-domain methods where the frequency content of recorded signals is manipulated [57-60] and ii) time-domain methods where the recorded ground motions amplitude is controlled [61, 62]. Regardless of the method, first, one or more time histories are selected subjectively, and then scaling mechanisms for spectrum matching are applied. This is a trial and error procedure that leads artificial signals very far from real-earthquake time series.
In this investigation a Genetic Generator of Signals is presented. This genetic generator is a tool for finding the coefficients of a pre-specified functional form, which fit a given sampling of values of the dependent variable associated with particular given values of the independent variable(s). When the genetic generator is applied to synthetic accelerograms construction, the proposed tool is capable of i) searching, under specific soil and seismic conditions (within thousands of earthquake records) and recommending a desired subset that better match a target design spectrum, and ii) through processes that mimic mating, natural selection, and mutation, producing new generations of accelerograms until an optimum individual is obtained. The procedure is fast and reliable and results in time series that match any type of target spectrum with minimal tampering and deviation from recorded earthquakes characteristics.
The objective of the genetic generator, when applied to synthetic earthquakes construction, is to produce compatible artificial signals with specific design spectra. In this model specific seismic (fault rupture, magnitude, distance, focal depth) and site characteristics (soil/ rock) are the first set of inputs. They are included to take into consideration that a typical strong motion record consists of a variety of waves whose contribution depends on the earthquake source mechanism (wave path) and its particular characteristics are influenced by the distance between the source and the site, some measure of the size of the earthquake, and the surrounding geology and site conditions; and that the design spectra can be an envelope or integration of many expected ground motions that are possible to occur in certain period of time, or the result of a formulation that involves earthquake magnitude, distance and soil conditions. The second set of inputs consist of the target spectrum, the period range for the matching, lower- and upper-bound acceptable values for scaling signal shape, and a collection of GAs parameters (a population size, number of generations, crossover ratio, and mutation ratio). The output is the more success individual with a chromosome array generated from “real” accelerograms parents (a set of).
The algorithm (see Figure 10) is started with a set of solutions (each solution is called a chromosome). A solution is composed of thousands of components or genes (accelerations recorded at the time), each one encoding a particular trait. The initial solutions (original population) are selected based on the seismic parameters at a site (defined previously by the user): fault mechanism, moment magnitude, epicentral distance, focal depth, geotechnical and geological site classification, depth of sediments. If the user does not have a priori seismic/site knowledge, the genetic generator could select the initial population randomly (Figure 11). Once the model has found the seed-accelerogram(s) or chromosome(s), the space of all feasible solutions can be called accelerograms space (state space). Each point in this search space represents one feasible solution and can be “marked” by its value or fitness for the problem. The looking for a solution is then equal to a looking for some extreme (minimum or maximum) in the space.
According to the individuals’ fitness, expressed by difference between the target design spectrum and the chromosome response spectrum, the problem is formulated as the minimization of the error function, Z, between the actual and the target spectrum in a certain period range. Solutions with highest fitness are selected to form new solutions (offspring). During reproduction, the recombination (or crossover) and mutation permits to change the genes (accelerations) from parents (earthquake signals) in some way that the whole new chromosome (synthetic signal) contains the older organisms attributes that assure success. This is repeated until some user’s condition (for example number of populations or improvement of the best solution) is satisfied (Figure 12).
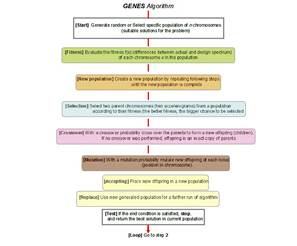
FIGURE 10.
Genetic Generator: flow diagram

FIGURE 11.
Genetic Generator: working phase diagram
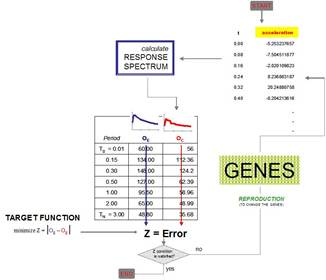
FIGURE 12.
Iteration process of the Genetic Generator
One of the genetic advantages is the possibility of modifying on line the image of the expected earthquake. While the genetic model is running the user interface shows the chromosome per epoch and its response spectra in the same window, if the duration time, the highest intensities interval or the ∅t∅tare not convenient for the user’s interests, these values can be modified without retraining or a change on model’ structure.
In Figure 13 are shown three examples of signals recovered following this methodology. The examples illustrate the application of the genetic methodology to select any number of records to match a given target spectrum (only the more successful individuals for each target are shown in the figure). It can be noticed the stability of the genetic algorithm in adapting itself to smooth, code or scarped spectrum shapes. The procedure is fast and reliable as results in records match the target spectrum with minimal deviation. The genetic procedure has been applied successfully to generate synthetic ground motions having different amplitudes, duration and combinations of moment magnitude and epicentral distance. Although the variations in the target spectra, the genetic signals maintain the nonlinear and nonstationary characteristics of real earthquakes. It is still under development an additional toolbox that will permit to use advanced signal analysis instruments because, as it has been demonstrated [63] [64], studying nonstationary signals through Fourier or response spectra is not convenient for all applications.
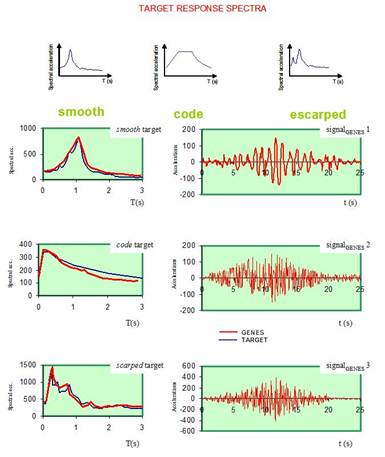
FIGURE 13.
Some Generator results: accelerograms application
EFFECTS OF LOCAL SITE CONDITIONS ON GROUND MOTIONS
Geotechnical and structural engineers must take into account two fundamental characteristics of earthquake shaking: 1) how ground shaking propagates through the Earth, especially near the surface (site effects), and 2) how buildings respond to this ground motion. Because neither characteristic is completely understood, the seismic phenomenon is still a challenging research area.
Site effects play a very important role in forecasting seismic ground responses because they may strongly amplify (or deamplify) seismic motions at the last moment just before reaching the surface of the ground or the basement of man-made structures. For much of the history of seismological research, site effects have received much less attention than they should, with the exception of Japan, where they have been well recognized through pioneering work by Sezawa and Ishimoto as early as the 1930’s [65]. The situation was drastically changed by the catastrophic disaster in Mexico City during the Michoacan, Mexico earthquake of 1985, in which strong amplification due to extremely soft clay layers caused many high-rise buildings to collapse despite their long distance from the source. The cause of the astounding intensity and long duration of shaking during this earthquake is not well resolved yet even though considerable research has been conducted since then, however, there is no room for doubt that the primary cause of the large amplitude of strong motions in the soft soil (lakebed) zone relative to those in the hill zone is a site effect of these soft layers.
The traditional data-analysis methods to study site effects are all based on linear and stationary assumptions. Unfortunately, in most soil systems, natural or manmade ones, the data are most likely to be both nonlinear and nonstationary. Discrepancies between calculated responses (using code site amplification factors) and recent strong motion evidence point out serious inaccuracies may be committed when analyzing amplification phenomena. The problem might be due partly because of the lack of understanding regarding the fundamental causes in soil response but also a consequence of the distorted soil amplification quantification and the incomplete characterization of nonlinearity-induced nonstationary features exposed in motion recordings [66]. The objective of this investigation is to illustrate a manner in which site effects can be dealt with for the case of Mexico City soils, making use of response spectra calculated from the motions recorded at different sites during extreme and minor events (see Figure 6). The variations in the spectral shapes, related to local site conditions, are used to feed a multilayer neural network that represent a very advantageous nonlinear-amplification relation. The database is composed by registered information earthquakes affecting Mexico City originated by different source mechanisms.
The most damaging shocks, however, are associated to the subduction of the Cocos Plate into the Continental Plate, off the Mexican Pacific Coast. Even though epicentral distances are rather large, these earthquakes have recurrently damaged structures and produced severe losses in Mexico City. The singular geotechnical environment that prevails in Mexico City is the one most important factor to be accounted for in explaining the huge amplification of seismic movements [67-70]. The soils in Mexico City were formed by the deposition into a lacustrine basin of air and water transported materials. From the view point of geotechnical engineering, the relevant strata extend down to depths of 50 m to 80 m, approximately. The superficial layers formed the bed of a lake system that has been subjected to dessication for the last 350 years. Three types of soils may be broadly distinguished: in Zone I, firm soils and rock-like materials prevail; in Zone III, very soft clay formations with large amounts of microorganisms interbedded by thin seams of silty sands, fly ash and volcanic glass are found; and in Zone II, which is a transition between zones I and III, sequences of clay layers an coarse material strata are present (Figure 14).
FIGURE 14.
Accelerographic stations used in this study
Due to space limitations, reference is made only to two seismic events: the June 15, 1999 and the October 9, 1995. This module was developed based in a previous study (see section 4.2 of this Chapter) where the effect of the parametersEDED, FDFD and MwMw on the ground motion attenuation from epicentre to the site, were found to be the most significant [71]. The recent disaster experience showed that the imprecision that is inherent to most variables measurements or estimations makes crucial the consideration of subjectivity to evaluate and to derive numerical conclusions according to the phenomena behavior. The neuronal training process starts with the training of four input variables booked:EDED, FDFD and MwMw. The output linguistic variables are PGAh1PGAh1 (peak ground acceleration horizontal, component 1) and ,PGAh2,PGAh2 (peak ground acceleration, horizontal component 2) registered in a rock-like site in Zone I .The second training process is linked feed-forward with the previous module (PGA for rock-like site) and the new seismic inputs are Seismogenic Zone and PGArock and the Latitude and Longitude coordinates are the geo-referenced position needed to draw the deposition variation into the basin. This neuro-training runs one step after the first training phase and until the minimum difference between theSaSa and the neuronal calculations is attained. In Figure 15 some results from training and testing modes are shown.
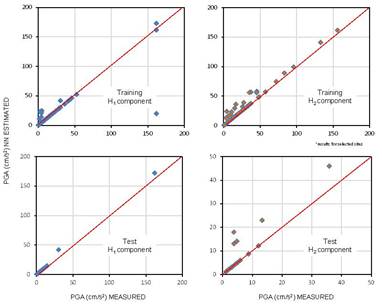
FIGURE 15.
Neural estimations for PGA in Lake Zone sites
This second NN represents the geo-referenced amplification ratio that take into consideration the topographical, geotechnical and geographical conditions, implicit in the recorded accelerograms.The results of these two NNs are summarized in Figure 16. These graphs show the predicting capabilities of the neural system comparing the measured values with those obtained in neural-working phase. It can be observed a good correspondence throughout the full distance and magnitude range for the seismogenic zones considered in this study for the whole studied area (Lake Zone).
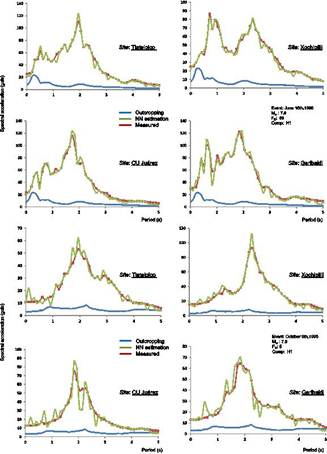
FIGURE 16.
Spectral accelerations in some Lake-Zone sites: measured vs NN
LIQUEFACTION PHENOMENA: POTENTIAL ASSESSMENT AND LATERAL DISPLACEMENTS ESTIMATION
Over the past forty years, scientists have conducted extensive research and have proposed many methods to predict the occurrence of liquefaction. In the beginning, undrained cyclic loading laboratory tests had been used to evaluate the liquefaction potential of a soil [72] but due to difficulties in obtaining undisturbed samples of loose sandy soils, many researchers have preferred to use in situ tests [73]. In a semi-empirical approach the theoretical considerations and experimental findings provides the ability to make sense out of the field observations, tying them together, and thereby having more confidence in the validity of the approach as it is used to interpolate or extrapolate to areas with insufficient field data to constrain a purely empirical solution. Empirical field-based procedures for determining liquefaction potential have two critical constituents: i) the analytical framework to organize past experiences, and ii) an appropriate in situ index to represent soil liquefaction characteristics. The original simplified procedure [74] for estimating earthquake-induced cyclic shear stresses continues to be an essential component of the analysis framework. The refinements to the various elements of this context include improvements in the in-situ index tests (e.g., SPT, CPT, BPT,VsVs), and the compilation of liquefaction/no-liquefaction cases.
The objective of the present study is to produce an empirical machine learning ML method for evaluating liquefaction potential. ML is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviours based on empirical data, such as from sensor data or databases. Data can be seen as examples that illustrate relations between observed variables. A major focus of ML research is to automatically learn to recognize complex patterns and make intelligent decisions based on data; the difficulty lies in the fact that the set of all possible behaviours given all possible inputs is too large to be covered by the set of observed examples (training data). Hence the learner must generalize from the given examples, so as to be able to produce a useful output in new cases. In the following two ML tools, Neural Networks NN and Classification Trees CTs, are used to evaluate liquefaction potential and to find out the liquefaction control parameters, including earthquake and soil conditions. For each of these parameters, the emphasis has been on developing relations that capture the essential physics while being as simplified as possible. The proposed cognitive environment permits an improved definition of i) seismic loading or cyclic stress ratio CSR, and ii) the resistance of the soil to triggering of liquefaction or cyclic resistance ratio CRR.
The factor of safety FS against the initiation of liquefaction of a soil under a given seismic loading is commonly described as the ratio of cyclic resistance ratio (CRR), which is a measure of liquefaction resistance, over cyclic stress ratio (CSR), which is a representation of seismic loading that causes liquefaction, symbolically, FS=CRR/CSRFS=CRR/CSR. The reader is referred to Seed and Idriss [74], Youd et al.[75], and Idriss and Boulanger [76] for a historical perspective of this approach. The term CSR CSR=f(0.65,ϡvo,amax,ϡ‘vo,rd,MSF)CSR=f0.65,ϡvo,amax,ϡvo’,rd,MSFis function of the vertical total stress of the soil ϡvoϡvo at the depth considered, the vertical effective stress ϡ‘voϡvo’, the peak horizontal ground surface acceleration amaxamax, a depth-dependent shear stress reduction factor rdrd (dimensionless), a magnitude scaling factor MSFMSF(dimensionless). For CRR, different in situ-resistance measurements and overburden correction factors are included in its determination; both terms operate depending of the geotechnical conditions. Details about the theory behind this topic in Idriss and Boulanger, [76] and Youd et al. [75].
Many correction/adjustment factors have been included in the conventional analytical frameworks to organize and to interpret the historical data. The correction factors improve the consistency between the geotechnical/seismological parameters and the observed liquefaction behavior, but they are a consequence of a constrained analysis space: a 2D plot [CSR vs. CRR] where regression formulas (simple equations) intend to relate complicated nonlinear/multidimensional information. In this investigation the ML methods are applied to discover unknown, valid patterns and relationships between geotechnical, seismological and engineering descriptions using the relevant available information of liquefaction phenomena (expressed as empirical prior knowledge and/or input-output data). These ML techniques “work” and “produce” accurate predictions based on few logical conditions and they are not restricted for the mathematical/analytical environment. The ML techniques establish a natural connection between experimental and theoretical findings.
Following the format of the simplified method pioneered by Seed and Idriss [74], in this investigation a nonlinear and adaptative limit state (a fuzzy-boundary that separates liquefied cases from nonliquefied cases) is proposed (Figure 17). The database used in the present study was constructed using the information included in Table 2 and it was compiled by Agdha et al., [77], Juang et al., [78], Juang [79], Baziar, [80] and Chern and Lee [81]. The cases are derived from cone penetration tests CPT, and shear wave velocities VsVs measurements and different world seismic conditions (U.S., China, Taiwan, Romania, Canada and Japan). The soils types ranges from clean sand and silty sand to silt mixtures (sandy and clayey silt). Diverse geological and geomorphological characteristics are included. The reader is referred to the citations in Table 2 for details.
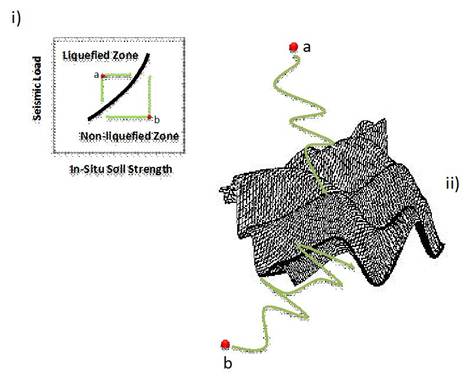
FIGURE 17.
An schematic view of the nonlinear-liquefaction boundary
The ML formulation uses Geotechnical (qcqc, VsVs, Unit weight, Soil Type, Total vertical stresses, Effective vertical stresses, Geometrical (Layer thickness, Water Level Depth, Top Layer Depth) andSeismological (Magnitude, PGA) input parameters and the output variable is “Liquefaction?” and it can take the values “YES/NO” (Figure 17). Once the NN is trained the number of cases that was correctly evaluated was 100% and applied to “unseen” cases (separated for testing) less than 10% of these examples were not fitted. The CT has a minor efficiency during the training showing 85% of cases correctly predicted, but when the CT runs on the unseen patterns its capability is not diminished and it asserts the same proportion. From these findings it is concluded that the neuro system is capable of predicting the in situ measurements with a high degree of accuracy but if improvement of knowledge is necessary or there are missed, vague even contradictory values in the analyzed case, the CT is a better option.
Figure 18 shows the pruned liquefaction trees (two, one runs using qcqc values and the other through theVsVs measurements) with YES/NO as terminal nodes. In the Figure 19, some examples of tree reading are presented. The trees incorporate soil type dependence through the resistance values (qcqc, andVsVs) and fine content, and it is not necessary to label the material as “sand” or “silt”. The most general geometrical branches that split the behaviors are the Water table depth and the Layer thickness but only when the soil description is based onVsVs, whenqcqc, serves as rigidity parameter this geometrical inputs are not explicit exploited. This finding can be related to the nature of the measurement: the cone penetration value contains the effect of the saturated material while the shear wave velocities need the inclusion of this situation explicitly. Without potentially confusing regression strategies, the liquefaction trees results can be seen as an indication of how effectively the ML model maps the assigned predictor variables to the response parameter. Using data from all regions and wide parameters ranges, the prediction capabilities of the neural network and classification trees are superior to many other approximations used in common practice, but the most important remark is the generation of meaningful clues about the reliability of physical parameters, measurement and calculation process and practice recommendations.
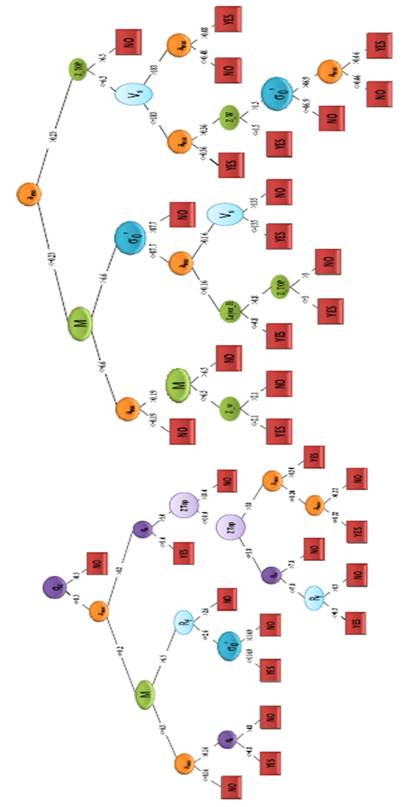
FIGURE 18.
Classification tree for liquefaction potential assessment
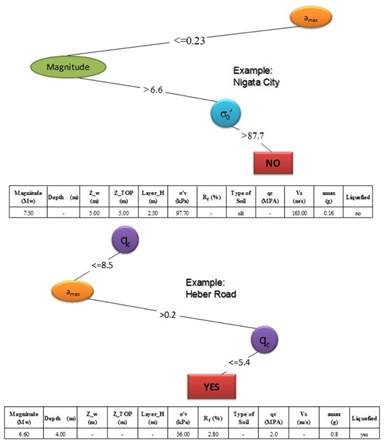
FIGURE 19.
CT classification examples
The intricacy and nonlinearity of the phenomena, an inconsistent and contradictory database, and many subjective interpretations about the observed behavior, make SC an attractive alternative for estimation of liquefaction induced lateral spread. NEFLAS [82], NEuroFuzzy estimation of liquefaction induced LAteral Spread, profits from fuzzy and neural paradigms through an architecture that uses a fuzzy system to represent knowledge in an interpretable manner and proceeds from the learning ability of a neural network to optimize its parameters. This blending can constitute an interpretable model that is capable of learning the problem-specific prior knowledge.
NEFLAS is based on the Takagi-Sugeno model structure and it was constructed according the information compiled by Bartlett and Youd [83] and extended later by Youd et al. [84]. The output considered in NEFLAS is the horizontal displacements due to liquefaction, dependent of moment magnitude, the PGA, the nearest distance from the source in kilometers; the free face ratio, the gradient of the surface topography or the slope of the liquefied layer base, the cumulative thickness of saturated cohesionless sediments with number of blows (modified by overburden and energy delivered to the standard penetration probe, in this case 60%) , the average of fines content, and the mean grain size.
One of the most important NEFLAS advantages is its capability of dealing with the imprecision, inherent in geoseismic engineering, to evaluate concepts and derive conclusions. It is well known that engineers use words to classify qualities (“strong earthquake”, “poor graduated soil” or “soft clay” for example), to predict and to validate “first principle” theories, to enumerate phenomena, to suggest new hypothesis and to point the limits of knowledge. NEFLAS mimics this method. See the technical quantity “magnitude” (earthquake input) depicted in Figure 20. The degree to which a crisp magnitude belongs to LOW, MEDIUM or HIGH linguistic label is called the degree of membership. Based on the figure, the expression, “the magnitude is LOW” would be true to the degree of 0.5 for aMwMwof 5.7. Here, the degree of membership in a set becomes the degree of truth of a statement.
On the other hand, the human logic in engineering solutions generates sets of behavior rules defined for particular cases (parametric conditions) and supported on numerical analysis. In the neurofuzzy methods the human concepts are re-defined through a flexible computational process (training) putting (empirical or analytical) knowledge into simple “if-then” relations (Figure 20). The fuzzy system uses 1) variables composing the antecedents (premises) of implications; 2) membership functions of the fuzzy sets in the premises, and 3) parameters in consequences for finding simpler solutions with less design time.
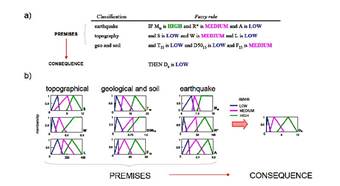
FIGURE 20.
Neurofuzzy estimation of lateral spread
NEFLAS considers the character of the earthquake, topographical, regional and geological components that influence lateral spreading and works through three modules: Reg-NEFLAS, appropriate for predicting horizontal displacements in geographic regions where seismic hazard surveys have been identified; Site- NEFLAS, proper for predictions of horizontal displacements for site-specific studies with minimal data on geotechnical conditions and Geotech-NEFLAS allows more refined predictions of horizontal displacements when additional data is available from geotechnical soil borings. The NEFLAS execution on cases not included in the database (Figure 21.b and Figure 21.c) and its higher values of correlation when they are compared with evaluations obtained from empirical procedures permit to assert that NEFLAS is a powerful tool, capable of predicting lateral spreads with high degree of confidence.
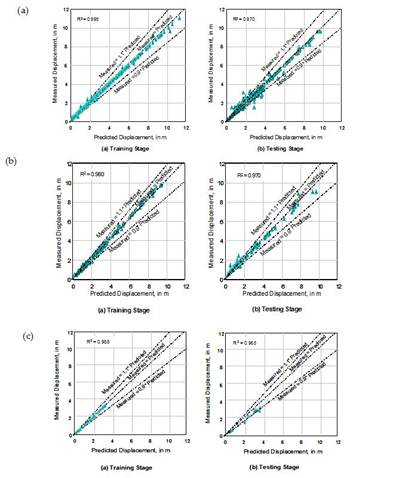
FIGURE 21.
NN estimations vs measured displacements for a) the whole data set, b)Niigata Japan, c) San Francisco USA cases
Conclusions
Based on the results of the studies discussed in this paper, it is evident that cognitive techniques perform better than, or as well as, the conventional methods used for modeling complex and not well understood geotechnical earthquake problems. Cognitive tools are having an impact on many geotechnical and seismological operations, from predictive modeling to diagnosis and control.
The hybrid soft systems leverage the tolerance for imprecision, uncertainty, and incompleteness, which is intrinsic to the problems to be solved, and generate tractable, low-cost, robust solutions to such problems. The synergy derived from these hybrid systems stems from the relative ease with which we can translate problem domain knowledge into initial model structures whose parameters are further tuned by local or global search methods. This is a form of methods that do not try to solve the same problem in parallel but they do it in a mutually complementary fashion. The push for low-cost solutions combined with the need for intelligent tools will result in the deployment of hybrid systems that efficiently integrate reasoning and search techniques.
Traditional earthquake geotechnical modeling, as physically-based (or knowledge-driven) can be improved using soft technologies because the underlying systems will be explained also based on data (CC data-driven models). Through the applications depicted here it is sustained that cognitive tools are able to make abstractions and generalizations of the process and can play a complementary role to physically-based models.