There are several methods exist to define the seismic performance levels of reinforced concrete (RC) structures. Among these methods, the nonlinear dynamic and the static analyses in which both methods involve sophisticated computational procedures because of the non-linear behaviour of the RCcomposite materials. In order to simplify these analyses for engineers, different suggested guidelines such as FEMA-356 (Federal emergency management agency [FEMA-356], 2000) and ATC-40 (Applied Technology Council [ATC-40, 1996]) were prepared to define the plastic hinges properties for RCstructures in the United States, and thus they have been used by many computer programs (i.e., ETABS [CSI, 2003], SAP2000 [CSI, 2008]) as a default or ready plastic hinge documents. However, there are still contradictions exist in the available literature due to the use of these ready documents in which the buildings are not designed based on the earthquake code of United States. The assessment of seismic performance of structures under future earthquakes is an important problem in earthquake engineering (Abbas, 2011). The use of methods and assumptions to define the seismic performance levels of RCbuildings become more and more important issue with time dependent effects of corrosion. Moreover, to the knowledge of the author, no any study has been performed up to date, which studies define the possible difference in the time-dependent seismic performance levels of RC buildings under the impact of corrosion by using default and user-defined plastic hinge properties.
The primary objectives of this study was to investigate the effects of default hinge properties based on FEMA-356 (FEMA-356, 2000) and user-defined hinge properties on the time-dependent seismic performance levels of corroded RC buildings. An assumed corrosion rate was used to predict the capacity curve of the buildings by using default and user-defined plastic hinge properties as a function of time (t: 25 years, and t: 50 years). Two, four and seven stories of RC buildings were considered to represent the effects of default and user-defined hinge properties on story levels. For the modelling of user-defined hinge properties, the time-dependent moment-curvature relationships of structural members were predicted as a function of corrosion rate for two different time periods in order to perform push-over analyses, while default hinge properties were used for the other case based on the ready documents by FEMA-356 (FEMA-356, 2000). Then, the nonlinear time-history analyses for both corroded and non-corroded buildings were performed by using 20 individual earthquake motion records. Seismic performance levels of non-corroded buildings and predicted time-dependent seismic performance levels of corroded buildings were compared based on their story levels as a result of user-defined and default hinge properties. Limit–states at each performance levels (e.i. immediate occupancy, life safety, collapse prevention and collapse) were obtained. The obtained results were summarized to compare the differences in the results of seismic response of the buildings due to user-defined and default hinge properties for both corroded and non-corroded cases.
Nonlinear material modelling
It is vital to accurately determine the effects of corrosion on the seismic analyses of RC buildings. Mainly, corrosion causes loss in the cross sectional area of the reinforcement bars and reduction in bond strength between reinforcement bars and concrete. A study done by Sezen and Moehle (Sezen & Moehle, 2006) indicated that, slip deformations contributed 25% to 40% of the total lateral displacement in the case of non-corroded reinforcement bars. These displacements might be more dramatic by lowering the bond strength due to corrosion. For the user-defined plastic hinge properties, time-dependent bond-slip relationships can be taken into account by modifying the moment-curvature relationships. Modified target post-yield stiffness of each structural member ensures the bond-slip relationships in nonlinear analyses. However, in the case of assigning the default hinge properties, available programs are not capable to consider the bond-slip relationships as a consequence of corrosion effects. Thus, it is inevitable to obtain huge difference in the result of time-dependent seismic performance levels of analysed buildings by using the default hinge properties. Therefore, in this study, the reduction in cross sectional area of reinforcement bars only considered as a function of time which can be also obtained by using available computer software programs.
A corrosion rate of 2.79 µA/cm2 was assumed in order to predict the loss in the cross sectional area of reinforcement bars as a function of time where 0.0116 was used as a conversion factor of µA/cm2 into mm/year for steel. For the user-defined plastic hinge properties, the obtained time dependent loss in cross sectional area of reinforcement bars were used to predict the moment-curvature relationships of RC sections. Developed model by Kent and Park (Kent & Park 1971) was used to model the stress-strain relationships of confined columns. Fig. 1 shows the well known developed model by Kent and Park (Kent & Park 1971) which was adapted for modelling the stress-strain relationships of RC sections in this study. Basically, the developed model by Kent and Park (Kent & Park 1971), has two branches. For the ascending branch (A-B), the curve reaches to maximum stress level at a strain of 0.002. After reaching maximum stress, two other different braches occurs (B-C, B-D) where two straight lines indicate different behaviour of concrete for confined and unconfined concrete. For the descending branch of the curve assumed to be linear and its slope specified by determining the strain when the concrete stress is decreased to half of its stress value as suggested by Park et al. (Park et al, 1982).
Mander’s (Mander, 1984) model was used for each time periods (i.e., t: 25 years, and t: 50 years) for modelling the stress-strain relationships of steel as can be seen from Fig. 2. The developed model by Mander (Mander, 1984) includes linear elastic region up to yield, elastic-perfect-plastic region, and strain hardening region. The Mander’s model (Mander, 1984) has control on both strength and ductility where the descending branch of the curve that first branch increases linearly until yield point then the curve continues as constant. In order to model the material properties, the following required assumptions were ![]() made. The modulus of elasticity of concrete
made. The modulus of elasticity of concrete
MPa was calculated according to TS500 (TSI, 2000). The mechanical properties of steel in the analyses were selected according to TS500 (TSI, 2000), where the minimum rupture strength (fsu) was equal to 500 MPa, the yield strain (εy) was equal to 0.0021, the strain hardening (εsh) was equal to 0.008, the minimum rupture extension (εsu) was equal to 0.12% and the modulus of elasticity of steel (Es) was taken as 200,000 MPa.
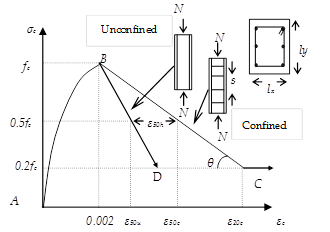
FIGURE 1.
Used stress-strain relationship of concrete (Kent & Park 1971).
Description of structures
Three RC buildings having two, four and seven stories were considered in this study. The assessed three RC buildings were selected among the typical constructed RC buildings in North Cyprus where the buildings were designed according to Turkish earthquake code (TEQ, 1997). The soil classes were classified as soft clay (group D), the building importance factor was taken as 1, and the effective ground acceleration coefficient (A0) was taken as 0.3g (seismic zone 2) according to Turkish earthquake code (TEQ, 1997). The buildings were remodelled to select the most critical frames by using the existing plans of the buildings. Fig. 3 shows the three dimensional modelling of a two story of RC building. In Fig. 3, the total height of the building is 6 m where the typical floor height is identical and equal to 3 m. The slab thicknesses of the building are same and equal to 0.15 m. The dead (G) and live (Q) loads of the slabs were designed to be 5.15 kN/m2 and 1.96 kN/m2, respectively. Additional wall load on the beams were designed to be 3.19 kN/m2.
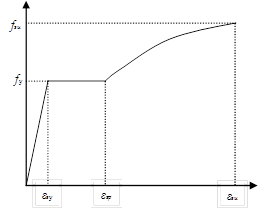
FIGURE 2.
Stress-strain relationship of steel (Mander, 1984).

FIGURE 3.
Three dimensional view of two story reinforced concrete building.
Fig. 4 shows two dimensional view of the selected frame from the two story of RC building. In Fig. 4, the member names and sectional dimensions of columns and beams with the amount of longitudinal reinforcement bars are also represented. The vertical distributed loads that were used in the analyses are also depicted in Fig. 4. The frame has a first-mode period of T1: 0.40 seconds having a total weight of 19.69 tons. For the second case study, a four story RC building was selected to be analysed which represents a typical apartment buildings in North Cyprus. Figs. 5 and 6 show three dimensional view and the selected frame of the building, respectively. In Fig. 5, the total height of the building is equal to 12 m where the typical floor height is identical and equal to 3 m. The slab thicknesses of the building are same and equal to 0.17 m. The dead and live loads on the slabs are 5.64 kN/m2 and 1.96 kN/m2, respectively. Additional wall load on the beams are identical and equal to 3.19 kN/m2. In Fig. 6, the sectional dimensions of all beams are identical and equal to 0.25 m by 0.60 m, with the same details of reinforcement bars. The frame has a first-mode period of T1: 1.09 seconds having a total weight of 55.53 tons.
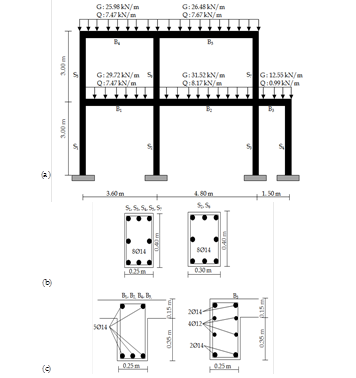
FIGURE 4.
Dimensional and reinforcement details of a two story frame: (a) Used vertical loads in the analyses, (b) Reinforcement details of columns, (c) Reinforcement details of beams.

FIGURE 5.
Three dimensional view of a four story RC building.

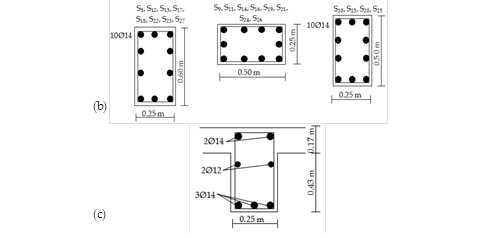
FIGURE 6.
Dimensional and reinforcement details of a four story frame: (a) Used vertical loads in the analyses, (b) Reinforcement details of columns, (c) Reinforcement details of beams.
The third case study deals with an existing seven story of a RC building. Figs. 7 and 8 show three dimensional view and the selected frame of the analysed building, respectively. In Fig. 7, the total height of the building is equal to 27 m where the typical floor height is identical and equal to 4.50 m. The slab thicknesses of the building are same and equal to 0.17 m. The dead and live loads on the slabs were 6.25 kN/m2 and 4.90 kN/m2, respectively. Additional wall load on the beams were identical and equal to 3.19 kN/m2. Because of having more than twenty different reinforcement details of beams, only reinforcement details of columns are shown in Fig. 8. In Fig. 8, the depicted vertical distributed loads of seventh floors are same for other floors. The frame has a first-mode period of T1: 4.27 seconds having a total weight of 151.56 tons.

FIGURE 7.
Three dimensional view of a seven story of RC building.
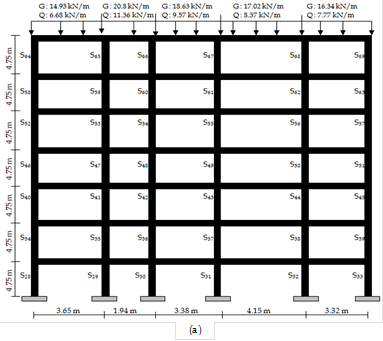
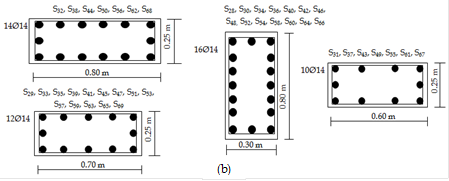
FIGURE 8.
Dimensional and reinforcement details of seven story of frame: (a) Used vertical loads in the analyses, (b) Reinforcement details of columns.
Moment-curvature relationships
Moment-curvature relationships were predicted in order to define the user-defined plastic hinge properties as a function of time. Moment-curvature relationships of columns were carried out from the calculated section properties and constant axial forces acting on the elements. Axial loads on the beams were assumed to be zero. A total of 210 plastic hinge properties as a function of time (t: 0 (non-corroded), t: 25 years, t: 50 years) were defined to be used in the nonlinear static push-over analyses. In order to predict the moment-curvature relationships, a new developed software program SEMAp (Inel et al., 2009) was used. SEMAp (Inel et al., 2009) models the stress-strain relationships of steel and concrete by the user. Fig. 9 shows the predicted moment-curvature relationships of randomly selected RC columns and beams as a function of time for different story levels. In Fig. 9, time dependent moment-curvature relationships of the assessed RC members basically indicates three segments; the elastic region prior to cracking, the post-cracking branch between the cracking and yield points and the post-yield segment beyond yielding, respectively. As shown in Fig. 9, premature yielding occurs due to the loss in cross sectional area of the reinforcement bars. For instance, for the same story level, the premature yielding moments of the S1 column corresponding to time periods of 25 and 50 years were 18% and 39%, respectively. As shown in Fig. 9, at the same moment values, curvature of a structural section increases as a function of time which affects the demand capacity of the frame by the defined plastic hinge properties.
In Fig. 9, the area under moment-curvature represents the storage energy capacity of a section in inelastic behaviour. As shown, in Fig. 9, the area under the curvature decreases due to premature yielding of reinforcement bars which causes cracking of concrete at early stages. The results of time period of 50 years showed that concrete crushes before the reinforcing bars exceed the strain hardening region with increased corrosion level.
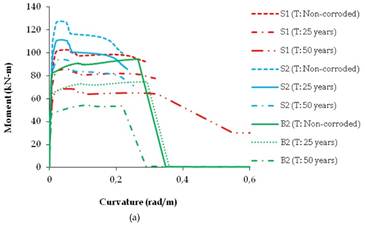
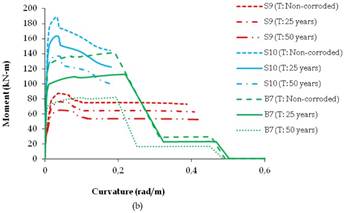
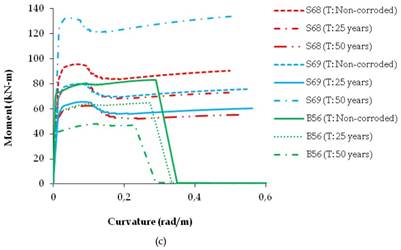
FIGURE 9.
Moment-curvature relationships of RC members as a function of time: (a) Two story, (b) Four story, (c) Seven story.
Nonlinear static analysis
SAP2000 (CSI, 2008) computer program was used to analyse the selected frames as a function of time. For the user-defined plastic hinge properties, the force-deformation behaviour needs to be plotted to define the behaviour of plastic hinges. Fig. 10 shows a typical force-deformation relationship to define the behaviour of plastic hinges by FEMA-356 (FEMA-356, 2000) and also the required acceptance criteria of immediate occupancy (IO), life safety (LS), collapse prevention (CP) and collapse (C).
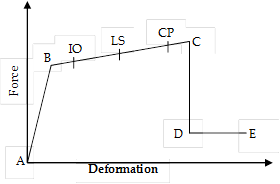
FIGURE 10.
Force-deformation relationship of a plastic hinge.
In Fig. 10, point A corresponds to unloaded condition of hinge deformation. Point B represents yielding of structural elements that controlled by moment-curvature relationships. Hinge deformation shows strength degradation at point D where the structure might show sudden failure after this point. The failure of the structure can be defined by reaching the point D and E. In this study, the locations of the hinges of the selected frames were located according to the study done by Inel and Ozmen (Inel & Ozmen, 2006). The lengths of the plastic hinges were used to calculate the moment-rotation instead of moment-curvature given by Eq. 1

where θ is the rotation of plastic hinge, Lp is the plastic hinge length, and ϕ is the curvature at a point.
There are different proposed models available in the literature to calculate the length of the plastic hinges. Since the mechanical properties of reinforcement bars play an important role for the user-defined plastic hinge properties, proposed model by Paulay and Priestley (Paulay & Priestley, 1992) to calculate the length of plastic hinges was used according to the given Eq. 2.

where L is the critical distance from the critical section of the plastic hinge to the point of contra flexure, fy and db are the yield strength and the diameter of longitudinal reinforcement bar, respectively.
As shown in Eq. 2, the proposed model by Paulay and Priestley (Paulay & Priestley, 1992) is important to ensure the effect of corrosion on the length of plastic hinges as a function of time. Shear strength hinge properties were calculated by using Eq. 3 according to ACI 318 code (ACI 318, 2005):
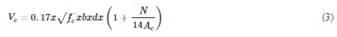
where Vc is the shear strengths provided by concrete, b is the section width, d is the effective depth, fc is the unconfined concrete compressive strength, N is the axial load on the section, and Ac is the concrete area.
The calculated plastic hinge properties were assigned to each floor at both ends of the beams and columns of the assessed frames according to the corresponding time periods. Triangular lateral load pattern was applied to the frames to perform nonlinear push-over analyses. There are different options are available in SAP2000 (CSI, 2008) to define the loading of the hinge properties. In this study, unload entire structure option was selected for the method of hinge unloading. When the hinges reach point Cin Fig. 10, the program continues to increase the base shear force. After point D the lateral displacement begins to reduce with the reduced base shear force and the structural elements starts to be unloaded. Fig. 11 shows the predicted time-dependent push-over analyses of the selected frames as a function of time for both of user-defined and default hinge properties.
As can be seen from Figs. 11a-c, the collapse mechanisms of non-corroded frames were affected by corrosion as a function of time. For instance, by using the user-defined plastic hinge properties, the collapse mechanism of the non-corroded frame of the two story of RC building started at a top displacement of 0.2633 m when the base shear force was 206 kN (see Fig. 11a). However, for the time periods of 25 and 50 years, collapse mechanism started at top displacements of 0.2608 m and 0.2612 m when the base shear forces were 170 kN and 130 kN, respectively. Same behaviour can be also observed for other performed frames. When the results were compared for the default hinge properties, the effect of corrosion can be also observed. However, there is a huge difference for the collapse mechanism of the assessed frames by default hinge properties. For instance, the time period of 50 years of the seven story of a RC building (see Fig. 11c), the recorded top displacement by user-defined plastic hinge properties was 0.92 m when the base shear force was 217 kN. For the same time period of the seven story building (see Fig. 11c), the recorded top displacement by default hinge properties was 0.36 m when the base shear force was 137 kN. Thus, it is clear that the shear capacities obtained from default hinge properties gave underestimate results when compared with the user-defined hinge properties for each case and time periods. For the time period of 25 years, the hinge patterns of two, four and seven stories of frames are plotted in Fig. 12.
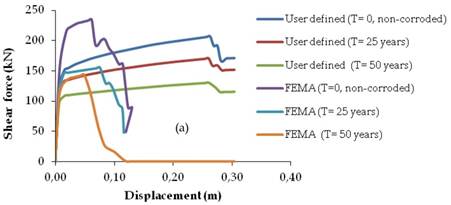
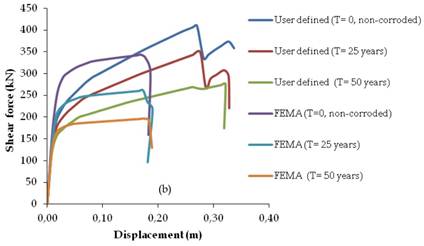
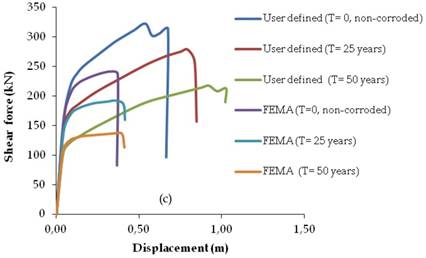
FIGURE 11.
Time dependent load-displacement relationships by using default and user defined plastic hinge properties: (a) Two story, (b) Four story, (c) Seven story.
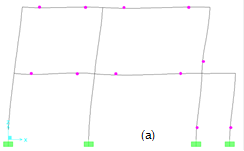
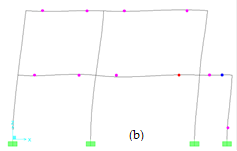
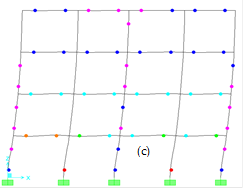
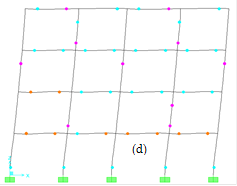
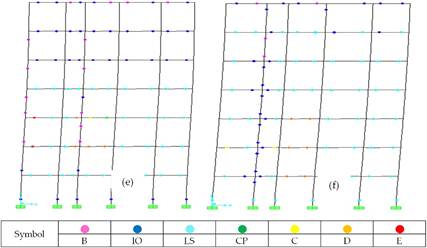
FIGURE 12.
Plastic hinge patterns by using default and user defined plastic hinge properties: (a) Two story user-defined, (b) Two story FEMA-356, (c) Four story user-defined, (d) Four story FEMA-356, (e) Seven story user-defined, (f) Seven story FEMA-356.
As can be seen from Fig. 12, significant differences in hinging by the user-defined and default hinge properties. By increasing the number of stories, the differences become more significant. In both plastic hinge properties, plastic hinge formations at both columns and beams show almost similar behaviour for a two story of RC frame. However, for upper stories, hinge formations especially in columns show significant differences. Non-linear time history analyses were performed in the following section to define the effects of both plastic hinges modelling on performance levels.
Seismic performance analyses
Incremental dynamic analyses (IDA) were performed to predict the performance levels of the assessed frames as a function of corrosion rate by the using user-defined and default hinge properties. For IDA, the 5% damped first-mode spectral acceleration (Sa (T1, 5%)) was selected. Twenty ground motion records were used to predict the performance levels of the building as a function of time. For the current study, the associated roof drift ratios corresponding to performance levels, IO, LS and CP were adopted from the study done by Stanish et al. (Stanish et al., 1999) and reduced drift values of 0.5%, 1%, and 2% were used for IO, LS, and CP, respectively. In order to perform IDA, NONLIN (Charney, 1998) a software computer program was used. By using the NONLIN (Charney, 1998), the material nonlinearity could be taken into account by specifying the yield strength and initial and post yield stiffness, which were calculated from the time-dependent load-displacement relationships (see Fig. 11). Twenty ground motion records were used to predict the performance levels of the buildings as a function of time, where the randomly selected motions records of pseudo velocity versus to period in seconds are shown in Fig. 13., where earthquake moment magnitudes (M) ranged from 4.7 to 7.51, PGA varied from 0.016 to 0.875g, and peak ground velocity (PGV) ranged between 1.65 to 117 cm/sec.
Figs. 14a-c, 15a-c and 16a-c show fragility curves of two, four and seven stories of RC buildings, respectively. In Figs. 14, 15 and 16, the obtained time dependent fragility curves which were in terms of PGA, compare the differences in the results of performance levels of the buildings as consequences of user-defined and default hinge properties.
The obtained fragility curves indicated that the performance levels of RC structures obtained by the default hinge properties based on FEMA may under-estimate or over-estimate results. Moreover, in the case of corroded conditions, the response of the buildings obtained by the default hinge properties does not represent the actual behaviour of the structures due to ductility problems of the structural members. Although the collapse mechanism of structures were affected by corrosion; directly reduced cross sectional area of reinforcement bars to perform ready documents hinge properties based on FEMAmight provide more ductile structural members which might also over-estimate results in the performance levels of RC structures. For instance in Fig. 14b, when the PGA is equal to 0.4g, the probability of exceeding the limit state corresponding to LS is 11% for user-defined plastic hinge properties while this probability is 2% based on FEMA ready documents plastic hinge properties. Such differences can be also observed in the case of non-corroded conditions. From Fig. 15a, it can be seen that, when the PGA is equal to 0.4g, the probability of exceeding the limit state corresponding to IO is 43% for the user-defined plastic hinge properties while this probability is 23% based on FEMA ready documents plastic hinge properties. It should be noted that for any story level, the maximum story displacements thus roof drift ratios occurred at different times according to user-defined or ready documents plastic hinge properties. Moreover, the results clearly showed that, the percentage of errors (i.e., IO, LS, CP) occurred due to use ready document plastic hinge properties were not proportional with story levels.
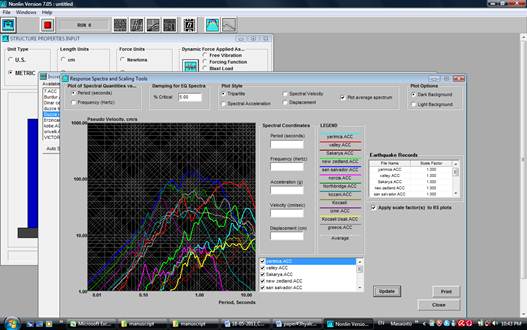
FIGURE 13.
Pseudo velocity spectrum for used ground motion records.
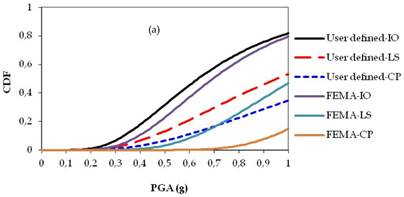
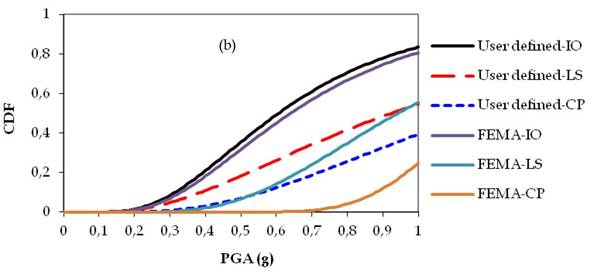
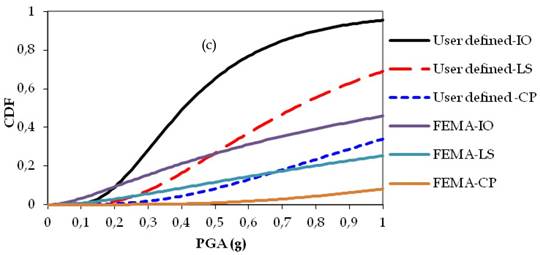
FIGURE 14.
Fragility curves of two story RC building: (a) Non-corroded, (b) T: 25 years, (c) T: 50 years.
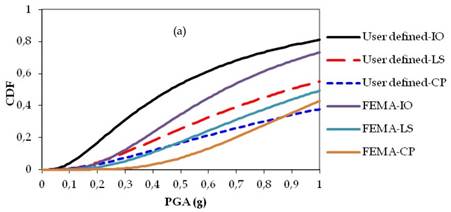
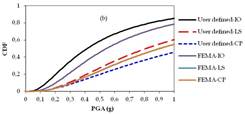
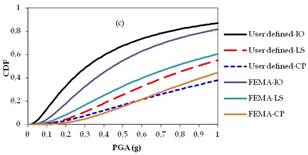
FIGURE 15.
Fragility curves of four story RC building: (a) Non-corroded, (b) T: 25 years, (c) T: 50 years.
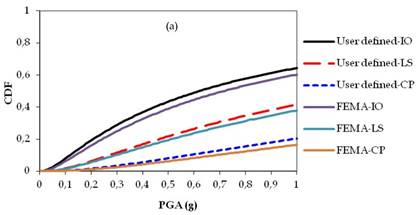
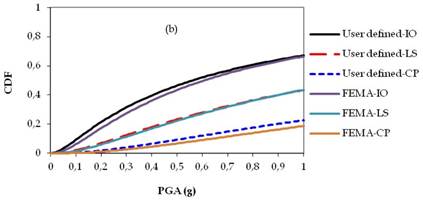
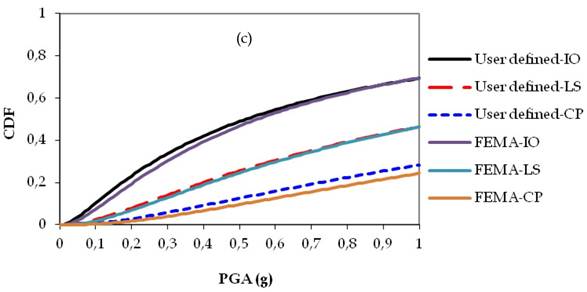
FIGURE 16.
Fragility curves of seven story RC building: (a) Non-corroded, (b) T:25 years, (c) T:50 years.
Conclusion
Incremental dynamic analyses for three RC buildings having 2, 3 and 7 stories were carried out as a function of time. The performed push-over analyses and IDA clearly showed that there were important differences due to the use of the plastic hinge properties based on ready documents and user defined hinge properties. If the user knows the capability of the program where SAP2000 (CSI, 2008) automatically stops the analysis when a plastic hinge reaches its curvature capacity, ready document plastic hinge properties might be used for rapid and preliminary assessment of RC buildings. However, the obtained time dependent results clearly showed that the user defined plastic hinge properties give better and correct results than default hinge properties. Additional studies are also required for accurate performance assessment of multi-degree-of-freedom systems. Bond-slip relationships and cover cracking of concrete due to corrosion need to be taken into account in seismic analyses where the effect of additional displacement due to slippage of reinforcement bars can be provided by the modification of plastic hinge properties. When the effects of corrosion on seismic performance levels and economical impacts in construction industry are considered, time-dependent nonlinear models rather than walk-down surveys are required for better decision making of strengthening of RC buildings to prevent serious damage under the expected seismic motions.



Comments are closed