A small diameter footing, of about 1 metre width, can normally be assumed to distribute the contact stress evenly over the footing contact area. However, this cannot be assumed to be the case for wider footings. Both the Boussinesq and the Westergaard distributions assume ideally flexible footings (and ideally elastic soil), which is not the case for real footings, which are neither fully flexible nor absolutely rigid and soils are only approximately elastic in loading. Kany (1959) and Steinbrenner (1934; 1936) showed that below a so-called characteristic point, the vertical stress distribution is equal for flexible and rigid footings. In an ideally elastic soil, the characteristic point is located at a distance of 0.13B and 0.13L in from the side (edge) of a rectangular footing of width, B, and length, L, and at a distance of 0.08R in from the perimeter of a circular footing of radius R. The distances from the center are 0.37 times B or L and 0.42 times the circle radius, respectively, i.e., about 0.4 times width, length, or diameter of either a footing or circle. Thus, when applying Boussinesq method of stress distribution to a regularly shaped, more or less rigid footing, the stress below the characteristic point is normally used rather than the stress below the center of the footing to arrive at a representative stress distribution for the settlement calculation. Indeed, with regard to vertical stress distribution, we can live with the fact that footings are not ideally flexible or rigid and natural soils are far from perfectly elastic.

The calculations by either of Boussinesq or Westergaard methods are time-consuming. The 2:1 method is faster to use and it is therefore the most commonly used method in engineering practice. Moreover, the 2:1 distribution lies close to the Boussinesq distribution for the characteristic point. However, for calculation of stress imposed by a loaded area outside its own footprint, the 2:1 method cannot be used. Unfortunately, the work involved in a “hand calculation” of stress distribution according the Boussinesq or Westergaard equations for anything but the simplest case involves a substantial effort. To reduce the effort, before-computer calculations were normally restricted to involve only a single or very few loaded areas. Stress history, e.g., the local preconsolidation effect of previously loaded areas at a site, was rarely included. Computer programs are now available which greatly simplify and speed up the calculation effort. In particular, the advent of the UniSettle program (Goudreault and Fellenius 2011) has drastically reduced the routine calculation effort even for the most complex conditions and vastly increased the usefulness of the Boussinesq and Westergaard methods.

Example.

Fig. 1.8 illustrates the difference between the three stress calculation methods for a square flexible footing with a side (“diameter”) equal to “B” and loaded at its center, and, forestalling the presentation in Chapter 3, Fig. 1.9 shows the distribution of settlement for the three stress distributions shown in Fig. 1.8. The settlement values have been normalized to the settlement calculated for the distribution calculated according to the Boussinesq method.

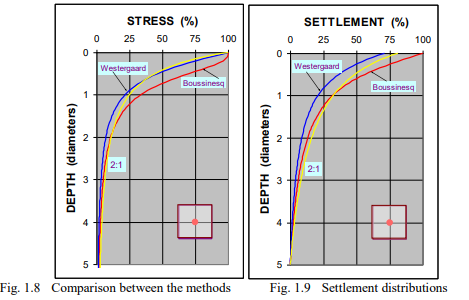
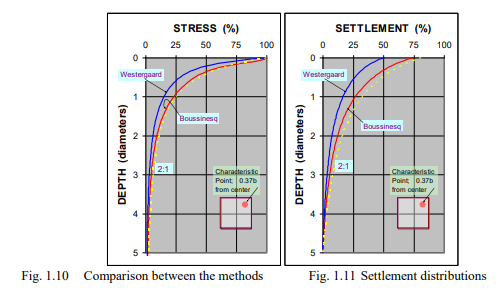
Figs. 1.10 and 1.11 shows the stress and settlement distributions for when the load is applied at the so-called characteristic point (x = y = 0.37B from the center of the footing), below which the stress distributions are the same for a flexible as for a rigid footing.

As illustrated in Fig. 1.12, calculations using Boussinesq distribution can be used to determine how stress applied to the soil from one building may affect an adjacent existing building.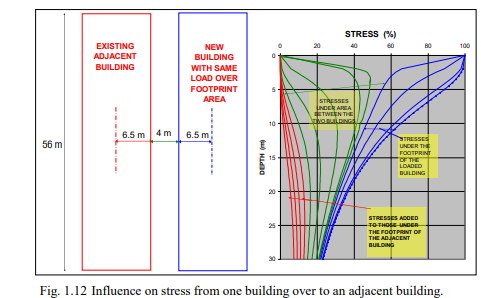

The stress exerted by the “existing building” is quite close to the preconsolidation margin of the soil, which means that the settlement is small. The “new building” exerts the same stress on the soil, and its stress adds to the stress from the existing building to the soils below this building, resulting in additional settlement for the “existing building”. At the same time, the settlement due to the stress from the “existing building” acting under the footprint of the “new building” has already occurred when the “new building” is constructed. Therefore, the settlement of the new building will be smaller than that for the first building. The analysis of the second building settlement needs to consider that the first building reduced or eliminated the preconsolidation margin underneath the footprint of the new building. Simple stress calculations will make the problem and potential undesirable effect very clear