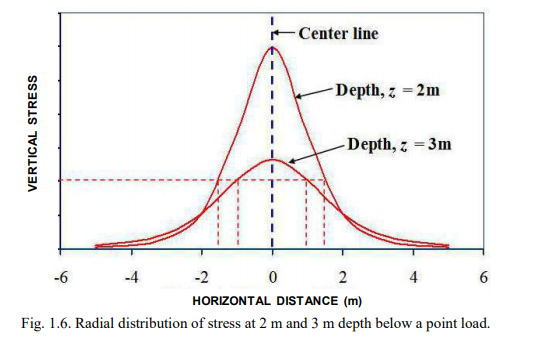
The assumption of ideally elastic response produces an exaggerated radial stress distribution near the location of the point-load. Thus, immediately below the location of a single point and to a distance radially away from the location, the Boussinesq point-load formula does not provide realistic values, as illustrated in Fig. 1.6. However, for a series of point-loads evenly spread out over an area and acting together, the sum (integration) of the errors of the point-loads will be compensated. Newmark (1935) integrated Eq. 1.15 over a finite area and obtained a relation, Eq. 1.17, for the stress, qz , under the corner of a uniformly loaded rectangular area, for example, a footing.

The A, B, and C relations shown below the equations, indicates when each equation controls, which are valid where m 2 + n2 + 1 £ m 2 n 2 . Notice that Eq. 1.17 provides the stress in only one point; for stresses at other points, for example when determining the vertical distribution at several depths below the corner point, the calculations have to be performed for each depth. To determine the stress below a point other than the corner point, the area has to be split in several parts, all with a corner at the point in question and the results of multiple calculations summed up to give the answer. Indeed, the relations are rather cumbersome to use. Also restricting the usefulness in engineering practice of the footing relation is that an irregularly shaped area has to be broken up in several smaller rectangular areas. Recognizing this, Newmark (1942) published diagrams called influence charts by which the time and effort necessary for the calculation of the stress below a point was considerably shortened even for an area with an irregularly shaped footprint.

Until the advent of the computer and spread-sheet programs, the influence chart was faster to use than Eq. 1.17, and the Newmark charts became an indispensable tool for all geotechnical engineers. Others developed charts using the Boussinesq basic equation to apply to non-rectangular areas and nonuniformly loaded areas, for example, a uniformly loaded circle or the trapezoidal load from a sloping embankment. Holtz and Kovacs (1981) and Holtz et al. 2011) include several references to developments based on the Boussinesq basic relation.

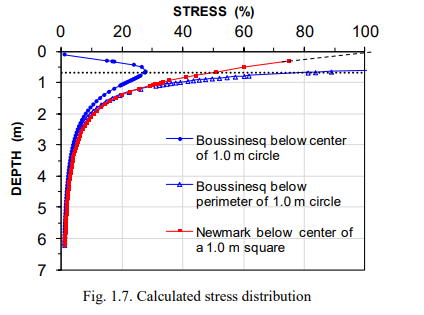
Figure 1.7 shows two stress distributions calculated using Eq. 1.15 (Boussinesq) and one using Eq. 1.17 (Newmark). The point-load stress distributions are calculated as a point-load equal to the total load integrated from a 1.0-m diameter circle stressed by 100 kPa with one distribution below the point load and one 0.5 m off to the side (i.e., below the circle perimeter). The Newmark stress distribution is calculated for the corner of a 0.5-m square area with a stress of 100 kPa. Multiplying the four corner values provides the stress distribution below the center of a 1.0-m square footing.