Steel-concrete composite bridges had a strong growth in railways and highways since the construction system provides an efficient and cost-effective form. The combination of steel and concrete in a single composite structural element enhances the individual advantages of both materials. By utilizing the tensile strength of steel in the main girder and the compressive strength of concrete in the slab, the bending resistance of the combined materials is greatly increased and larger spans are made possible. It allows overcoming difficulties caused by irregular orography and offers advantages in terms of resistance and ductility useful in high seismicity areas.

The chapter, precisely, concerns with a steel-concrete composite viaduct on a territory with a variable orography and focuses on the dissipation method of the seismic energy.

The context, which led to the choice of hydraulic devices with the stabilizer system, is analysed. Such devices, designed according to the stiffness of the substructures, allowed to limit and, partly, dissipate the stresses, induced by the earthquake, maintaining the underlying structures substantially elastic to the condition of LLS. Then, the checks have proven the capacity of the structures to support the stresses to limit state condition (LSC) without undergoing any damages, assuring curving capacity of the piers. The implementation of the devices has been preceded by the timely check of the functionality of the same and of the correspondence of the project-operating curve in accordance with the provisions of the pertaining European regulation, among which EN15129:2009 [1] as well as the Italian standard DM 14/01/2008 [2].

MAIN FEATURES OF THE VIADUCT

The viaduct covers a total length equal to 1102 m and it is made up of 15 spans, divided as follows: 68.0 + 75.0 m × 13 + 59.0 m. The piers have a maximum height of 65 m and present remarkable variability from one span to the other.

The slab is 12.0 m large and harbours a 10.5-m large lane. The main girders, 2.96 m high, have a distance of 7 m and they are linked by bracing each 6.50 m; a lower cross-bracing system provides resistance against torsional effects. This type of structure is lightweight, easy to transport and it permits easy launch.

The choice of the steel-concrete composite structure with continuous deck well adapts to the alignment and altimetric irregularities assuring reduced seismic masses at the same pace with a suitable stiffness.

The vertical structures are represented by reinforced concrete piers with pseudo-ellipsoid hollow section, with an average thickness ranging from 30 to 45 cm. Drilled piles with a diameter equal to 1.5 m, featuring a suitable resistance to side forces, in terms of both shear stress and induced bending stress, have been used for foundation structures. Such a choice is supported by the breaking strength test, carried out in the worksite, where the same piles have proven to assure and move a greater peak flow compared to the piles, having an equal length and a smaller diameter. The design has been performed in compliance with the capacity design, focusing on the plastic reserves of the structure in correspondence of the dissipation devices and of the piers (keeping the superstructure, the vertical support devices and the foundations in the elastic range).

OROGRAPHY CONTEXT

The viaduct is inserted in a context of deep narrow valleys, not serviced at all, and features a territory with constant lithological characteristics (although variable from a geotechnical point of view for the different compaction of the layers), where the surface of the grey-deep blue clays is from time to time covered with layers of loose yellow sand or by the relating remodelled layers of the main geological formations. Together with geotechnical irregularities, there are also some altimetric irregularities, ordered by the alignment with connection and curve areas. These irregularities affected the project choices as for both the type of construction and the earthquake-resistant system (Figure 1).

FIGURE 1.

Orography of the site.

CHOICE OF THE EARTHQUAKE-RESISTANT SYSTEM

Given the remarkable irregularity of the height of the piers and of the road alignment, it was necessary to couple the longitudinal oscillation of the deck and the oscillation of the underlying piers. Such coupling has been induced on the higher piers (having a similar stiffness) by the introduction of OT (shock-transmitter) devices. The lower piers have been left free to oscillate, whereas those with an intermediate height have also been coupled with hydraulic thermoplastic devices with OTP viscous-type behaviour able to control the forces, conveyed to the underlying piers. Transversally, plastic hydraulic OP-type devices as well as fixed restraints have been used. Such a choice implies that the piers or the devices, alternatively, must be able to dissipate the energy of the earthquake by any formation of plastic hinges or the work expressed by the devices. In compliance with the project, with regard to seismic testing, the types of joints, able to allow the displacements during both the service and earthquakes, have been defined.

Both fluid viscous dampers and shock transmitters are integrated with bearings. They have been designed according to the different stiffness of the substructures and allow limiting and partially dissipating the stresses induced by the earthquake, keeping the deck and the substructures substantially elastic for life-safety limit state condition (at the ultimate limit state (ULS)).

The installation of the devices was preceded by the accurate analysis of their seismic behaviour and matching of functional curves with the design assumptions, in accordance with the dictates of the European Reference Standards including UNI EN15129:2009 [1] as well as the mandatory Italian Standard ‘D.M. 14/01/2008’ [2, 3]. Finally, dynamic tests were carried out in situ to validate the theoretical assumptions about the dynamic behaviour of the real decks and substructures (Figures 2 and 3).

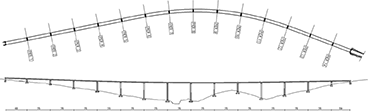
FIGURE 2.

Viaduct plan and view.

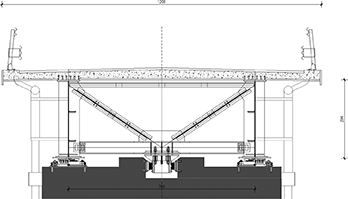
FIGURE 3.

Viaduct cross section.

Modelling and design approach

The design of the viaduct was performed according to Italian code [2, 3] taking into account the dissipative behaviour of the structural elements, material and geometric non-linearity, following a high-ductility approach.

The dissipative zones are concentrated in the seismic-restraint devices while non-dissipative elements are designed according to capacity design criterion [2, 3]. The structure is conceived and designed with the goal to create a stable dissipative mechanism under the seismic action at the life-safety limit state (ultimate limit state—ULS).

The plastic deformations of the base of the piers generate displacement demand that is requested to be lower than the capacity of the system. The comparison between ductility demand and available ductility was carried out on the basis of the instructions provided in [4]. In detail, deck, vertical support devices, foundation structures and abutments are designed to remain elastic.

‘Over-strength’ factors were considered for the verification of the pier sections outside the plastic hinge region and for the foundations as well. The fixed constraint devices were dimensioned according to the capacity design criterion. The dissipative devices were designed to support, without collapse, earthquake displacements caused at the collapse limit state (CLS).

The computational analysis has been carried out using finite element method (FEM). The model of the viaduct is of a three-dimensional type (Figure 4) and recreates the stiffness of the structural elements, constituting it, the non-linear features are concentrated within the restraint devices and at the base of the piers (plastic hinges). It takes into account geometric and material non-linearity.

FIGURE 4.

Finite element model.

For the piers, a moment-curvature constitutive law has been adopted by using the Takeda model [5]. The model represents the hysteretic features of reinforced concrete structures by means of the trilinear relation force displacement (Figure 5a), where the non-linearity is modelled by using concentrated plastic hinges and takes into account cracking and yielding. From the force-displacement law, it is possible to retrieve the corresponding moment-curvature link. Such assessment has been carried out distinctly for each pier. With this choice, it is possible to assess in the transient state the stiffness change of the substructures, checking the consequent redistribution of the stresses among the following piers of the viaduct.

The OP and OTP viscous dissipation devices are devices provided with a cylinder and a piston, depending on the velocity, where the lamination of a silicone fluid by means of a suitable hydraulic circuit allows energy dissipation. The typical constitutive law force-velocity, simulating the behaviour is of non-linear type (Figure 5b), is

where C represents the damping constant and α is assumed to be equal to 0.15.

The dissipation devices have been modelled by means of spring-damper elements with the association of the law force-velocity (Eq. (1)). There are two types of devices, a plastic OP hydraulic one and the other one is an OTP thermal-plastic hydraulic one.

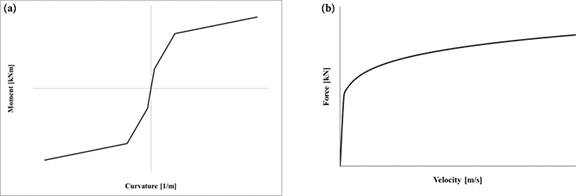
FIGURE 5.

(a and b) Flow chart moment curvature according to Takeda and force-velocity law (F = C × V^α).

The OT devices, with a dynamic restraint (shock transmitter), represent a very stiff restraint against a dynamic action, whereas they allow slow displacements of the structures (e.g. due to thermal changes). Owing to their features, they have been modelled as truss elements with a high stiffness.

DESIGN CHOICES RELATING TO RESTRAINT DIAGRAM

FIGURE 6.

Restraint diagram.

The restraint system is outlined in Figure 6. Longitudinally, the fixed piers (P7 and P8) absorb static stresses due to braking and play the role of a thermal centre point by means of a transversal one-way restraint; from a seismic point of view, the shorter piers (P–P3 and P14 with a height of less than 25 m) are free to oscillate, piers P3–P13 (about 30 m high) are provided with OTP-type dissipation devices, able to check the stress value, given by the deck; for the remaining piers (with height exceeding 35 m), the application of temporary-restraint devices (shock-transmitter OT) is provided. Transversally, the piers (P1–P4, P10, P13, P14) are provided with a multidirectional support, associated to an OP plastic hydraulic type device, whereas P5, P6, P9, P11, P12 are associated with a DEF* (*with shoes, able to accept longitudinal displacements) fixed type restraint; piers P7 and P8 are provided with a transversal one-way support device, associated with a DEF-type device. From a seismic point of view, only the piers, being less than 35 m high (P1–P4, P10, P13, P14), have been isolated. The classification diagram of the piers is represented in Figure 7.

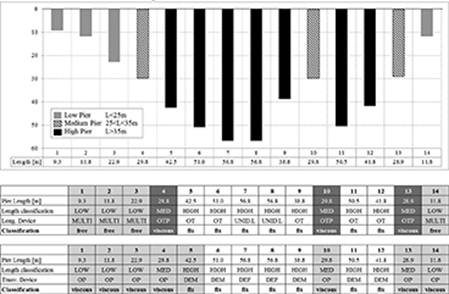
FIGURE 7.

Piers classification diagram.

ANALYSES PERFORMED

The assessment of the actions, due to the earthquake, has been carried out by means of a non-linear dynamic analysis with step-by-step integration. The masses associated to gravitational loads have been assessed as follows:

where G₁ is the weight of the structure; G₂ is the permanent load; Q_j is the traffic load.

The procedure adopted provides for

·         – Non-linear step-by-step dynamic analysis (three groups of accelerograms in the three directions applied simultaneously). The effects on the structure are represented by the most adverse values of the effects obtained by the analysis by using the three different groups of accelerograms for ULS.

·         – Linear step-by-step dynamic analysis for comparison with non-linear step-by-step analysis in order to establish the structure factor q, implicitly deriving from the hysteretic cycle of load-unload of the materials, making up the substructures. With such q value, then, the over-strength factor, required for the check of the sections, placed outside of the critical areas, has been calculated (capacity design).

·         – Modal analysis with design spectrum (using the estimated q) and approval of the non-linear step-by-step analysis by comparison with the total forces at the base of the piers.

For seismic purposes, the following parameters (referred to DM 14/01/2008 [2]) have been taken into account: rated life of the works, VN = 50 years; use coefficient of the works, CU = 2. The result is a reference period equal to V_R = 100 years. The soil has been considered of class C: deposits of medium thickened soil, with layers of more than 30m where mechanical properties gradually increase with depth.

3. Analysis results and match with test data

The results of the seismic computational analyses are shown in the following charts. They are presented as a comparison between theoretical and experimental data. The former are characterized by the law of materials and devices deriving from mathematical assumptions, the latter instead use the output results of the laboratory-type test (Figure 8). The constitutive diagram of the piers, shown in Figure 9, remains the same in both analyses.

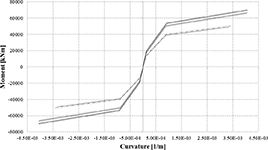
FIGURE 8.

Comparison between theoretical and type-test law for devices.

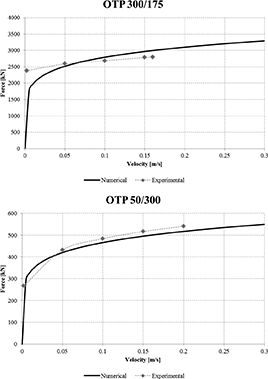
FIGURE 9.

Constitutive diagrams of the piers.

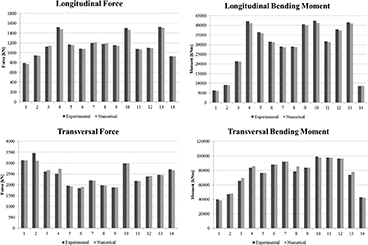
FIGURE 10.

Representative bar charts of the forces and moments at the base of the piers—comparison between experimental and numerical results.

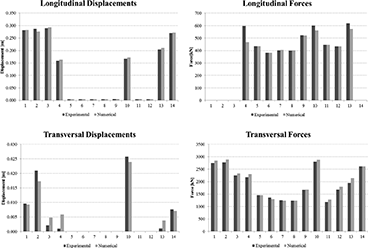
FIGURE 11.

Bar charts representing forces and displacements on the level of the devices—comparison between experimental and numerical results.

The results of the non-linear analyses are represented here below; each chart shows by the most adverse effects of three accelerograms at the ULS applied as explained in Section 2.2 (Figures 10 and 11).

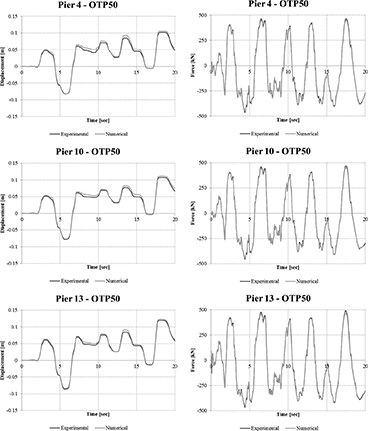
FIGURE 12.

Charts displacement versus time and force versus time of the OTP and OP devices—comparison between experimental and numerical results.

FIGURE 13.

Diagrams longitudinal moment curvature at the base of the piers—comparison between experimental and numerical results.

It is easy to find the substantial congruence of the two analyses in terms of forces and displacements, which in the diagrams in Figure 12 are compared in a time history analysis.

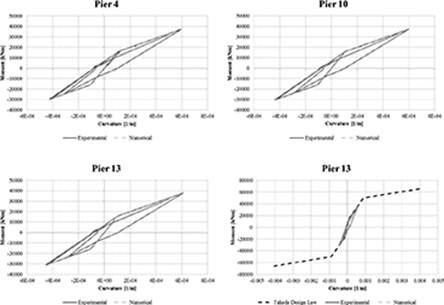
FIGURE 14.

Sum of the forces at the base of the piers (in kN)—estimation of the structure factor.

From the moment-curvature diagrams of Figure 14, it is, moreover, possible to verify how the piers remain substantially elastic, dissipating energy only for the cracked range without yielding the metal rebars.

The non-linear analysis has been carried out by considering the constitutive law of concrete piers (Figure 9), so a comparison with a linear analysis is necessary in order to assess and confirm the structure factor, adopted in the verifications. The structure factor is equal to q = 1.5 and derives from the ratio of the summation of the shear force at the base of each pier (Figure 13).

The superstructure is requested to remain elastic during the seismic event. To control this requirement, the set of largest transversal displacements relating to the top of the piers has been applied to an accurate finite element model of the deck, where the girders and the slab are represented with shell elements, the bracing system are modelled with linear element and the devices are springs characterized by their stiffness.

The displacement set is the output of the non-linear analysis, with a peak of 0.33 m at the pier 7 (Figure 15).

It follows the calculation of stresses on the steel elements (Figure 16), where it is notable that the stress level is lower than the yielding limit.

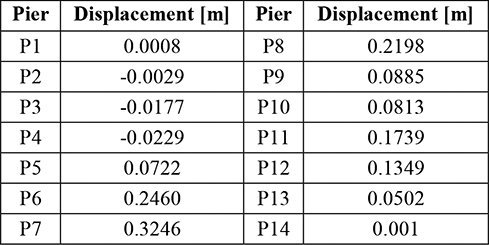
FIGURE 15.

Transversal displacement of the piers applied to the FEM model.

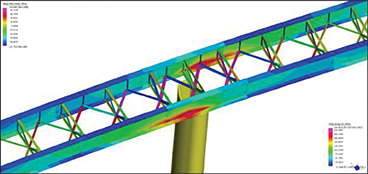
FIGURE 16.

Stresses on the steel elements.

Conclusions

Construction methods and seismic protection techniques are interesting topics regarding multi-span viaducts characterized by steel-concrete composed deck.

A detailed design leads to the solution of many issues deriving from the structural altimetric and planimetric irregularity and from the high seismicity of the site.

The analyses have been performed applying the capacity design approach. Dissipative devices have been used against the seismic forces in order to grant and control that the piers remain substantially elastic.

For such purpose, each pier has been modelled taking into account its non-linear behaviour (theory of Takeda), simulating the stiffness at the cracking and plastic deformation status, in terms of moment curvature.

It has been verified that the system displacement request is lower than its capacity; the comparison between the ductility requested and the ductility available for the piers has been carried out according to the instructions provided by EC8-2 Annex E.

By the application of such design philosophy, it was possible to limit the forces at the base of the piers and, on the other side, the displacements of the decks and of the top of the same piers; the linear behaviour requirement of the metal superstructure under the effect of the seismic action was fulfilled as well.

At last, the comparison between the results of the FEM analysis performed using numerical and experimental data highlighted the correctness of the design hypothesis assumed.