Many methods have been proposed for mitigating the harmful effects of strong earthquakes. The conventional approach requires that structure passively resist through a combination of strength, deformability and energy absorption. The level of damping in these structures is typically low. During earthquakes, these structures deform well beyond the elastic limit and remain intact due to their ability to deform inelastically. The inelastic deformation takes the form of localised hinges, which results in an increased flexibility and energy dissipation. Therefore, much of the earthquake energy is absorbed by the structure through localised damage of lateral force-resisting system.

An alternate approach to mitigate the hazardous effects of earthquakes is based on a consideration of the distribution of energy within a structure. The input energy from the ground acceleration is transformed into both kinetic and potential (strain) energy that must be either absorbed or dissipated trough heat. A large portion of the input energy, instead of being absorbed by hysteretic action (i.e. damage of the structure) can be dissipated with supplemental systems.

This approach to seismic energy dissipation is made clear by considering the following time-dependent conservation of energy relationship:

E(t) =Ek(t)+Ez(t)+Eh(t)+Ed(t)

(1)

where E is the absolute energy input from the earthquake motion, E_k is the absolute kinetic energy, E_s is the elastic (recoverable strain energy), E_h is the irrecoverable energy dissipated by the structural system through inelastic or other forms of action (hysteretic or viscous), E_d is the energy dissipated by a supplemental damping system and t represents the time.

The chapter analyses the seismic retrofit of an existing viaduct, by assessing an actually designed case study. The viaduct at issue, built during the Seventies, serving a fast-moving thoroughfare in the city of Naples (Italy), features reinforced concrete piers and a mixed steel-concrete box deck. Three solutions, corresponding to the most common types of interventions for earthquake protection, have been compared: the first by using hydraulic dissipation devices, the second using sliding pendulum isolator devices and the third by using elastomeric isolators. The differences have been compared according to traffic interferences, interferences with existing structures, operational needs and to time and costs necessary to achieve a final project solution.

THE VIADUCT MAIN FEATURES

The viaduct analysed, which already has an earthquake intervention in place, features a length of 1360m and a continuous deck on 18 spans with variable clearance from 62 to 92m, separated by four longitudinal joints, implemented with Gerber saddles to assure structural continuity (Figures 1 and 2). The reinforced concrete piers have a hollow circular section, with a variable base diameter ranging from 2.65 to 3.30m. They are vertically compressed and feature a variable height ranging from 7.90 to 38.80m. The foundations are deep, well and raft based with piles. The structural joints are located at the piers 4, 6, 11 and 14. One particular aspect of the viaduct is that there is only one support per each pier, placed at the central part of the box. Hence, the deck is balanced, since the two adjacent runways are connected by means of transverse girders at each support section (Figure 3).

Intervention on an existing work always requires special attention and a meticulous study. For example, with the viaduct under examination, the base of the piers is inaccessible for any type of reinforcement intervention. Additionally, it is not possible to stop traffic in order to replace the supports, and therefore, it is not possible to work on the abutments, to draw back the ballast retainers if a larger gap than the present one (measuring 15 cm) should be required. Moreover, the client wishes that the bearing system, present in the current situation, is respected, so that during all the installation phases of the new devices, the viaduct does not change its static operating conditions and above traffic can continue uninterrupted (represented in Figure 5).

FIGURE 1.

Viaduct plan.

FIGURE 2.

Viaduct view.

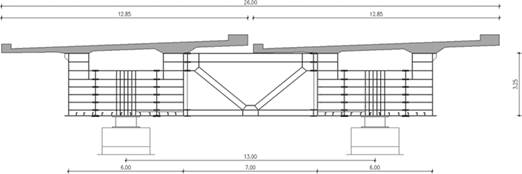
FIGURE 3.

Typical cross-section of the viaduct.

Modelling

The analyses have been carried out using a finite-element analysis software on a model, consisting in mono-dimensional elements; they are non-linear with step-by-step integration of the equations of motion.

For seismic purposes, the following parameters (Italian Standard DM 14.01.2008 [1, 2]) have been taken into account:

·         Rated life of the work: V_N = 50 years, relative to bridges and infrastructures;

·         Use coefficient: C_U = 2, corresponding to Use Class IV about strategic construction in case of calamity and bridges of particular importance after seismic events in order to keep communication ways available;

·         Reference life of the work equals to V_R=100 years; it comes from the product V_R = V_N·C_U;

·         Soil type C: deposits of medium thickened soil, with layers of more than 30m where mechanical properties gradually increase with depth; VS30 (average equivalent velocity of S wave in the first 30 m) range is 180—360 m/s;

·         Topographic coefficient T₁=1 that correspond to a flat surface.

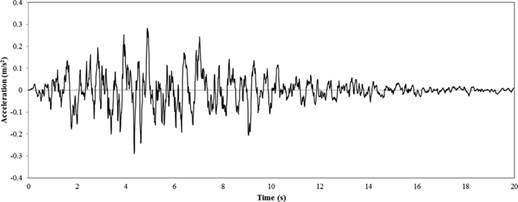
FIGURE 4.

Artificial accelerogram.

For the analysis, artificial spectrum-compatible accelerograms have been used (Figure 4). It is noted that the use of real accelerograms and spectrum-matching techniques, together with records selection tools, tends to be recommended for the derivation of suits of records for use in non-linear dynamic analysis of structures but in this case, the access to real accelerograms was challenging. In literature [3], it is shown that the structural response estimated by using simulated records generally matches the response obtained using recorded motions. The software can generate artificial time-histories of ground acceleration compatible with the target spectrum and gives a comparison between its response spectrum and the target spectrum itself (Figure 5).

The computational analysis has been carried out using finite-element method. The model of the viaduct is three-dimensional (3D) type (Figure 6), representing the stiffness features of the structural elements. The composing elements are all of linear elastic type, except for the restraint devices and for the base of the piers, where it is assumed that plastic hinges may form. It takes into account geometric and material non-linearity.

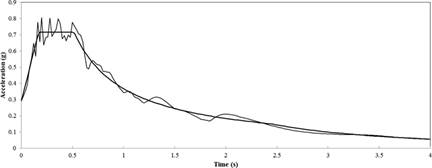
FIGURE 5.

Compatibility between response spectrum and target spectrum.

FIGURE 6.

Finite-element model.

For the piers, a moment-curvature constitutive law has been adopted by using the Takeda model [4]. The model represents the hysteretic features of reinforced concrete structures by means of the trilinear relation force-displacement, where the non-linearity is modelled by using concentrated plastic hinges and takes into account cracking and yielding. From the force-displacement law, it is possible to retrieve the corresponding moment-curvature link. Such assessment has been carried out distinctly for each pier. With this choice, it is possible to assess in the transient state the stiffness change of the substructures, checking the consequent re-distribution of the stresses among the following piers of the viaduct.

The support and restraint devices are represented by special elements where it is possible to specify stiffness in any of six degrees of freedom between two nodes. They do not behave like a standard beam element; the degrees of freedom are user specified and are independent of each other. For non-linear analysis, each stiffness value may be defined via a non-linear table: force-velocity type for hydraulic devices and force-displacement type for isolators.

The foundations of the piers and of the abutments are modelled with punctual restraints.

RESTRAINT SYSTEMS ANALYSIS

It follows a description of the three solutions of seismic protection that will be analysed and compared in the next paragraphs.

For every solution, in order to achieve a monolithic behaviour of the deck during the seismic event, the installation of shock transmitters at the Gerber saddle provides to hinder the relative movements of the box girders. Being a dynamic device, the shock transmitters allow slow displacements (thermal change) and represent a stiff restraint against dynamic actions. The new system remains unchanged in the static stage and becomes unique kinematic chain during the seismic stage.

The restraint systems analysed original scheme, fluid viscous dampers (explained in Section 2.1.1), curved surface sliding isolators (commented in Section 2.1.2) and elastomeric isolators (described in Section 2.1.3) and are outlined in Figure 5.

When the viscous damper is indicated, the number following the device type represents the force threshold at which the hydraulic system starts laminating the fluid (Figures 7 and 8).

FIGURE 7.

Bearing and restraint system.

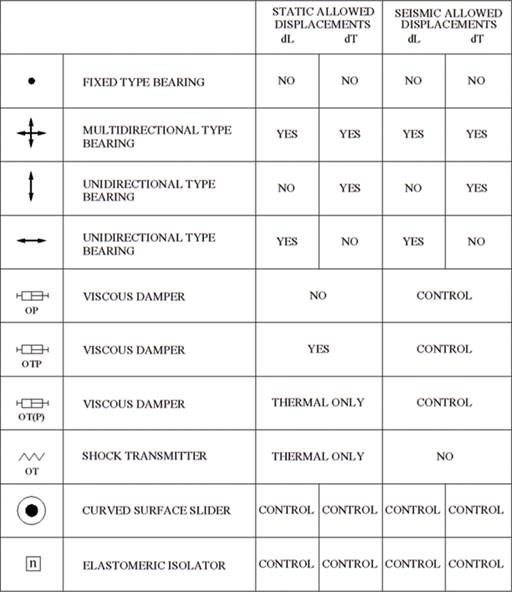
FIGURE 8.

Map legend.

HYDRAULIC DISSIPATION DEVICES

The system consists of a multidirectional-encapsulated neoprene support coupled with different types of hydraulic viscous devices. They work at a speed range compatible with those of the target seismic event.

When the system reaches the design velocity that corresponds to a force threshold (following the exponential law at Eq. (2)), the piston starts to laminate the silicone fluid and it allows increasing displacements while the force level, transferred to the substructure, is kept constant.

The oleodynamic-plastic (OP) devices provide a stiff restraint against static forces but dissipate the seismic energy. It means that they can control the force level transferred to the piers up to a design limit (about 100/150 tons).

The oleodynamic-thermal-plastic devices (OTP) permit thermal expansions without remarkable resistance; instead, during the seismic stage, they are able to dissipate energy above an imposed strength level (work as an OP for dynamic forces).

The OT(P) devices are able to act as an OP (providing stiffness and dissipating energy) for high-speed displacements, induced by impulsive forces of dynamic (earthquake) and static (wind and braking) source. They behave like an OTP for low-speed displacements (temperature changes) that are allowed. Its benefit is distributing operation forces, such as braking, on a greater number of piers, reducing the forces of the fixed central device of the train.

The constitutive equation force-velocity, which characterises them, is non-linear:

where C is the damping constant, v is the velocity and α is variable from 0.10 to 0.15, according to the device.

The OT (hydraulic-thermal) devices, finally, provide for a stiff restraint during the seismic event, acting as a fixed device, while allowing low-speed displacements in the static stage (thermal expansion).

All the parameters, used in the analysis, are specified in Chart 1 for each device.

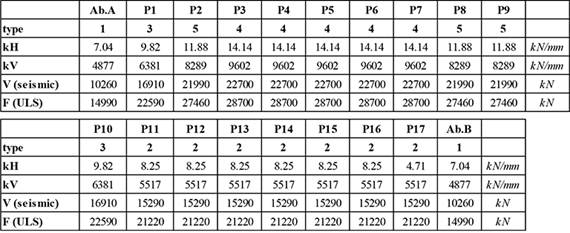
CHART 1.

Features of the elastomeric isolators used in the analysis. k_H is the horizontal stiffness, k_V is the vertical stiffness, V is the maximum vertical load at load combinations including the seismic action and F is the maximum vertical load at non-seismic load combination at ULS.

CURVED SURFACE SLIDING ISOLATORS

The curved surface sliders are sliding isolators based on the working principle of the simple pendulum. In a structure isolated by means of this device, the period of oscillation mainly depends on the radius of curvature of the curved sliding surface and it is almost independent from the mass of the structure.

The energy dissipation is provided by the friction, which develops during the sliding, and the re-centring capacity is provided by the curvature of the sliding surfaces.

These devices are characterised by two concave surface sliders whose radius of curvature impose the period of oscillation and accommodate for horizontal displacements and rotations. A special thermoplastic material coupled with stainless steel is used on both primary and secondary sliding surfaces to govern the friction.

The material, an ultra-high molecular weight polyethylene, grants an optimal behaviour in terms of load-bearing capacity, friction coefficient and consequently energy dissipation, durability and stability to hysteretic displacement cycles. It is used without lubrication on the primary sliding surface, while it is dimpled and lubricated on the secondary one.

The above-mentioned devices feature a maximum vertical load equal to N_Ed=2200t and allow displacements of ± 150mm, in the load combination that includes the seismic action or foresees a horizontal displacement.

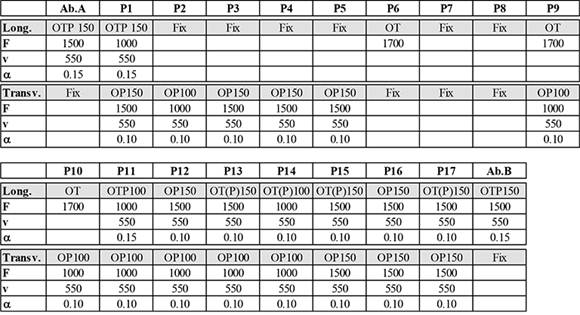
CHART 2.

Features of the viscous dampers used in the analysis.

The value of the minimum dynamic friction coefficient matching with the maximum vertical design load N_Ed of the isolator is equal to 2.5% and varies with the vertical load, acting on the isolator.

The constitutive equation force-displacement, which characterises them, is bilinear type:

where μ is the friction coefficient, N_Sdis the load acting on the isolator (quasipermanent load), R is the equivalent radius of curvature, and d is the displacement.

All the parameters, characterising the devices, are specified in Chart 2 since the vertical load on each support is different, being a continuous deck.

ELASTOMERIC ISOLATORS (NON-DISSIPATING)

This kind of isolators consists in a rubber bearing made up of layers of elastomer.

These devices are characterised by low horizontal stiffness, high vertical stiffness and negligible damping capacity. These characteristics permit to increase the fundamental period of vibration of the structure and to resist to vertical loads without appreciable settling.

The fundamental design parameters used to determine vertical and horizontal stiffness are the geometrical characteristics (overall dimensions and thickness) and the mechanical characteristics of the elastomeric compound that is characterised by an effective dynamic shear modulus G equal to 1.4 MPa.

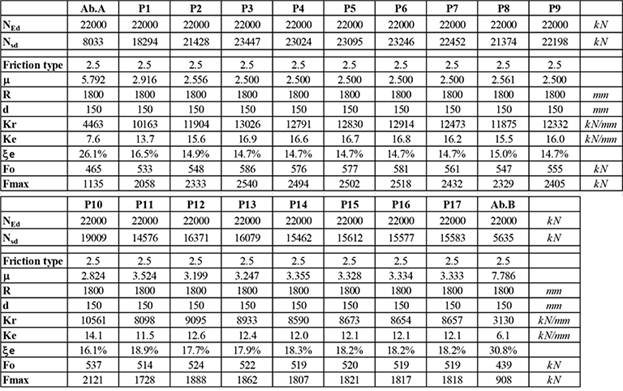
CHART 3.

Features of the sliding isolators used in the analysis. K_r is the restoring stiffness, K_e is the equivalent stiffness (in case of linear analysis), ξ_e is the effective viscous damping, F₀ is the friction force developed by the isolator and F_max is the maximum horizontal force.

The compounds contain suitable antiageing additives that guarantee limited variation of the physical and mechanical characteristics in time.

Their behaviour is modelled as linear by means of the equivalent stiffness. Five types of isolators have been defined. All the parameters, characterising the devices, are specified in Chart 3 since the vertical load on each support is different, being a continuous deck.

NON-LINEARITY CONSIDERED

According to the standards [1, 2], the structure needs to be designed in order to develop a stable dissipative mechanism, where dissipation is attributed to the piers (plastic hinges) or to appropriate devices. The elements not involved in the dissipative process need to remain elastic similar to the substructure of isolated bridges.

In this retrofit, the dissipation is committed to devices, and so it is necessary to check the behaviour of the base section of the piers.

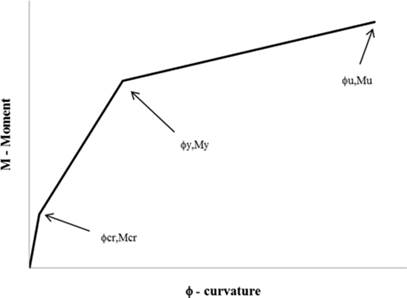
FIGURE 9.

Constitutive diagram of the piers.

The hysteretic model of Takeda has been selected to represent the non-linear behaviour of the concrete structures. It is a realistic conceptual model that recognises the continually varying stiffness and energy-absorbing characteristics of the structure. Three linear segments define the primary curves (Figure 9), and the first break refers to cracking. The yield load (end point of the second line) is obtained assuming a parabolic compressive stress-strain curve for the concrete. The yield deflection depends on the deflection caused by curvature based on cracked section, the shearing deflection and the deflection caused by slip of the reinforcement and depression of the concrete. The slope of the third segment is related to the strain-hardening properties of the reinforcement. The response under load reversal, depending on the displacement ductility and the axial load ratio, is explained in the study of Takeda et al. [4].

The dissipating devices have been modelled as springs and they have been characterised by their constitutive law, described in the previous paragraphs, that is force-velocity or force-displacement type (as shown in Figure 10).

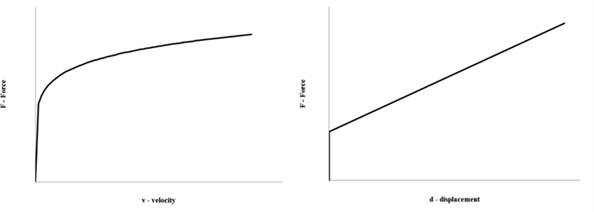
FIGURE 10.

Constitutive laws of dissipative devices, dampers and sliders.

The following charts recall the features of each device of the restraint diagrams outlined in Figure 5 and described in Sections 2.1.1 and 2.1.2 (Chart 4).

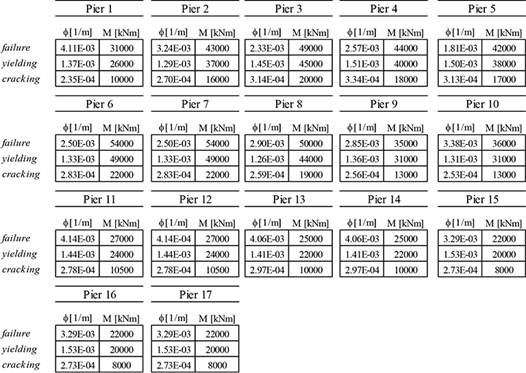
CHART 4.

Parameters of non-linear material characterising the constitutive law of the pier bases.

Results

The results of the analyses performed have been presented as a comparison among the restraint diagrams proposed, in terms of stresses at the base of the piers (Figures 11 and 12), displacements on the top of the pier (Figure 13), displacements and forces acting on the devices (Figures 14 and 15) and dissipated energy (Figures 16 and 17). The following charts relate to the maximum stresses for each base section of the piers. These results were assessed as the square root of the instant-by-instant stresses, since the pier is circular; the charts also show the values of the “yield moment” of the examined sections.

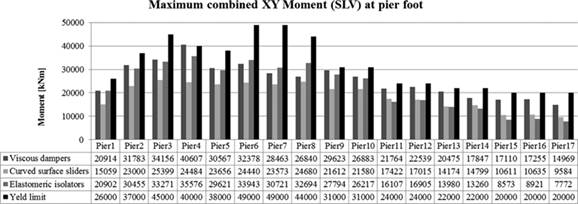
FIGURE 11.

Bar chart of the bending stresses ULS (max XY) at the base of the piers.

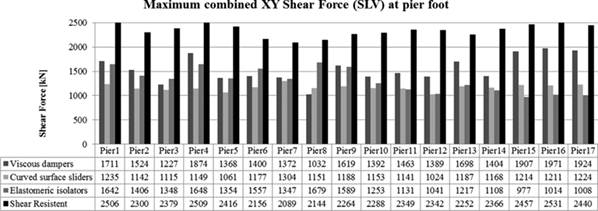
FIGURE 12.

Bar chart of the shear stresses ULS at the base of the piers.

As asserted in Section 2.2, the main requirements are to ensure that the substructure behaves elastically.

It can be deduced from Figure 11 how all the solutions lead to stress levels that are lower than the yield limit of the piers. Furthermore, the solution with viscous devices better exploits the bending-resistant capacity and the shear-resistant capacity of the reinforced concrete section.

The following chart refers to the displacement of pier top. This parameter is linked to the control of the local ductility at the plastic hinges [5] by the chord rotation. The latter is measured over the length of the pier, between the end section of the plastic hinge and the section of zero moment.

The verification that deformation demands are safely lower than the capacities of the plastic hinges should be performed by comparing plastic hinge rotation demands, θ_p,E, to the relevant design rotation capacities, θ_p,d, as follows: θ_p,E<θ_p,d.

Again, it is necessary to ensure that the displacements are lower than the yield displacement limit (Chart 5):

The following charts refer to devices, and in particular, they show displacements and the conveyed forces.

The chart in Figure 14 regards the displacements of the devices and to be understood it needs to be read together with the chart in Figure 15, which concerns about the stress level reached by the devices.

In general, the amount of the displacements increases when the height of the pier is low, due to the ductility of the element. Considering Figure 13, the displacement of the pier is greater for higher piers.

It is possible to affirm that for lower piers (from pier 11 to 17), the behaviour of sliders and elastomeric isolators in terms of strength is similar; while the displacement is different, the latter request more displacement than the former in order to guarantee the same level of force.

The displacements of OP-type dampers are null, and from the bar chart shown in Figure 13, it is possible to appreciate that the displacement of the top of the piers with fix restraint or OP restraint is greater.

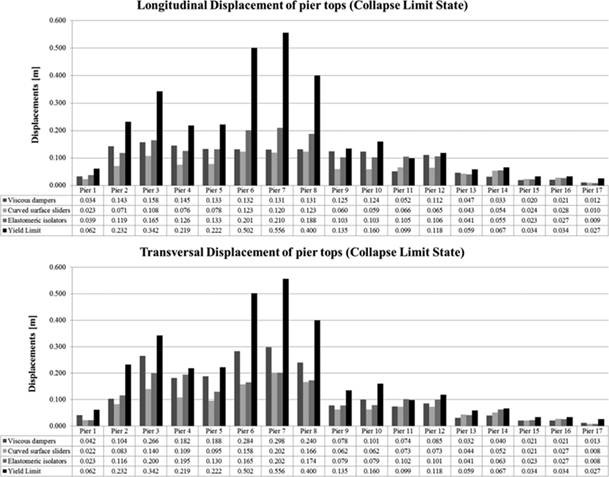
FIGURE 13.

Bar charts representing the displacements on the level of the heads of the piers.

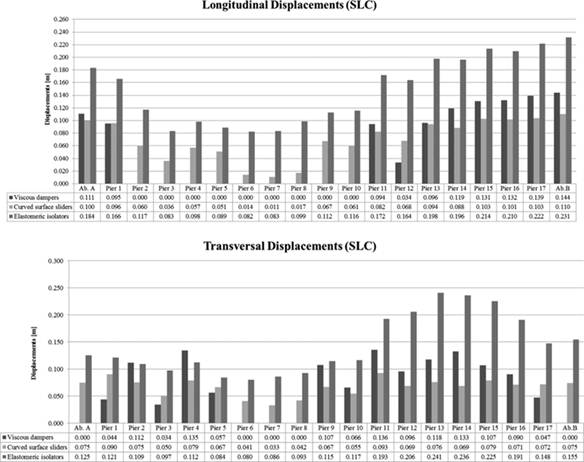
FIGURE 14.

Bar charts representing the displacements on the level of the devices.

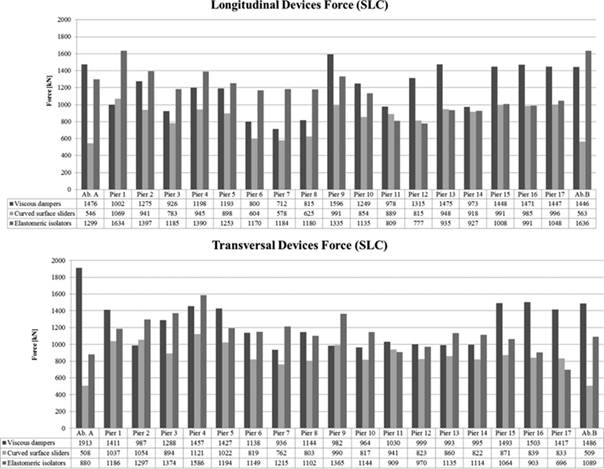
FIGURE 15.

Bar charts representing the forces on the devices.

The following diagrams contain the hysteretic energy dissipation processes of the following two main opposing mechanisms of the earthquake (devices and piers): the devices in terms of force-displacement (there is dissipation only in case of dampers and sliders) and the material of the piers, relating to the base section, in terms of moment-curvature. The area underlying the curves is an indicator of the dissipated energy.

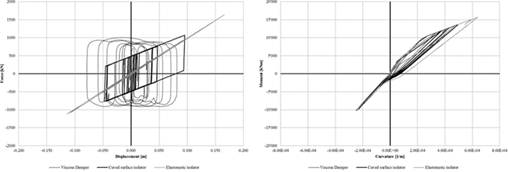
FIGURE 16.

Comparison of energy dissipation (restraint device and section at the base of the pier n.1 – earthquake ULS of Collapse).

The following chart (Figure 17) summarises the endeavour performed by the piers during the duration of the earthquake: the same is obtained as the sum of the products of forces at the base of the pier and the displacement at the top of the same pier for each moment of the seismic event. In particular, it is clear how the piers are implicated in the total dissipation process of the seismic energy, partly carried out also by the devices in terms of displacement. Moreover, it can be deduced how the solution with the sliders allows transferring only a reduced portion of energy to the piers.

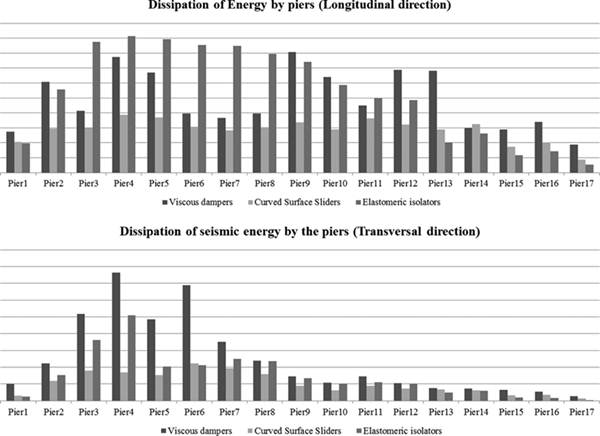
FIGURE 17.

Bar charts representing energy dissipation in the earthquake expressed by the piers.

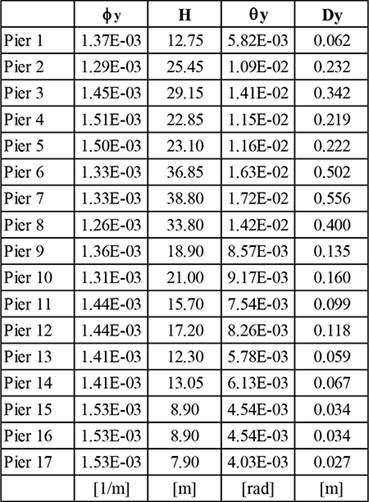
CHART 5.

Displacements correspondent to yield limit curvature of the pier.

Conclusion

The analysis focused on three different retrofit solutions of an existing viaduct, examining the technical aspects relating to the design of dissipation and isolation systems. When it is necessary to operate on existing structures, a special attention and carefully conceived solutions are mandatory. Regarding the actual design of the viaduct in question, the restraints are related to the impossibility of stopping traffic and to intervening by reinforcing the existing piers, respecting limitations imposed by the client regarding safety conditions during the implementation of the works.

GENERAL CONSIDERATIONS

All the solutions proposed have been designed and calibrated in order to respect the requirement of not using the plastic reserve of the piers, to contrast the forces induced by the system. The refining has related to the modulation of the operative velocity of the viscous devices, the definition of the curvature of the sliding isolators and the level of the stiffness of the rubber of the elastomeric isolators (as reported in Charts 1–3). The chart, in Figure 10, represents the comparison between the stressing actions and the yield limit of the substructures.

SOLUTION WITH FLUID DYNAMIC DISSIPATION DEVICES (SOL. 1)

The solution respects all the restraints desired by the client. It is not necessary to intervene by reinforcing the piers, the gaps on the abutments are assured (displacements less than 15 cm), the bearing system of the current situation even in the transient phase (during works) is assured and the structure is totally verified. Implementing this solution requires rather high implementation costs. In fact, it is necessary to remodel the top of each pier by widening the top to allow the housing of the contrast structures of the dissipating devices. Another relevant cost can be ascribed to the assembly of the same dissipating devices.

From a global point of view (not strictly engineering), this is the best solution as it allows a check of the stresses acting on the substructures, regardless of the intensity of the seismic event, at the expense of the displacement of the devices. The devices are provided by law with a safety margin to be able to tackle greater displacements compared to those for which they have been designed. Therefore, it is necessary to implement the joint gaps with a consistent safety margin in order to avoid hammering between the deck and the abutment structures.

SOLUTION WITH CURVE SLIDING ISOLATORS (SOL. 2)

The solution with the sliders is the most efficient, in regards to the stresses on the substructures and for the displacements during the seismic stage. But it does feature some issues in regards to the management of the bearing system during assembly, given that the actual fixed points of the deck are removed. During operation, although, for horizontal loads, due to vehicular traffic (braking) and to wind, the minimum friction allows to develop a breakaway torque (F₀) greater than the one, to which each support is subject, thermal expansion entails displacement at all the piers. This solution also allows a low implementation cost, since the support integrated the isolator, which features nearly the same sizes of the existing support.

From an engineering point of view, the solution is efficient and allows to involve in the dissipation process, both the piers (within the allowed capacity) and the devices (owing to the friction developed by the material interposed between the curved surfaces), with a work rate lower than the one required by the solution with only the dampers. Since the sliders is at the same time an isolator, the solution, moreover, allows enhancing the total response of the structure, defining a new oscillation period, independent from the deck mass but depending on the curvature of the devices. With reference to the modal analysis with the project spectrum, the structure undergoes a smaller seismic acceleration at the base, due to an increase in the period.

As far as realisation is concerned, the solution shortens the supply period (same type of device on all the piers), simplifies the launching operations for implementation, as the new devices feature sizes and space requirements similar to the existing supports. Yet, the type of support is not suitable for this specific viaduct, featuring a central point-shaped bearing. It entails the application of auxiliary temporary restraints, for the management of the transitory stage, which is not easy to implement.

SOLUTION WITH ELASTOMERIC ISOLATORS (SOL. 3)

The solution with elastomeric isolators is the less suitable option in this case. Although it allows not intervening on the piers, in regards to the base and heading sections, it involves more displacements than the previous solutions (thus requiring the widening of the gaps on the abutments, thus necessarily interfering with traffic circulation). As Sol. 2, it does not preserve the bearing system of the current situation in the transitory stage as desired by the client.

Yet, this solution has been analysed and compared, since it is one of the most widespread as for this type of intervention, and it is undoubtedly the cheapest.