Introduction
Before a foundation design can be embarked on, the associated soil profile must be well established. The soil profile is compiled from three cornerstones of information:
· assessment of the overall site geology
· in-situ testing results, particularly continuous tests, such as the CPTU
· laboratory classification and testing of recovered soil samples
· pore pressure (piezometer) observations
Projects where construction difficulties, disputes, and litigations arise often have one thing in common: borehole logs and soundings were thought sufficient when determining the soil profile, disregarding information on the geology.
The essential part of the foundation design is to devise a foundation type and size that will result in acceptable values of deformation (settlement) and an adequate margin of safety to failure (the degree of utilization of the soil strength). Deformation is due to change of effective stress and soil shear resistance is proportional to effective stress. Therefore, all foundation designs must start with determining the effective stress distribution of the soil around and below the foundation unit. That initial distribution then serves as basis for the design analysis. The “initial” condition may well be many years back in time and the long-term—final—condition years ahead in time.
Effective stress is the total stress minus the pore pressure (the water pressure in the voids). Determining the effective stress requires that the basic parameters of the soil are known. The basic parameters are the pore pressure distribution and the Phase Parameters, such as water content1 ) and total density. Unfortunately, far too many soil reports on site conditions lack adequate information on both the pore pressure distribution and the phase parameters.
Phase Parameters
Soil is an “interparticulate medium”. A soil mass consists of a heterogeneous collection of solid particles with voids in between. The solids are made up of grains of minerals or organic material. The voids contain water and gas. The water can be clean or include dissolved salts and gas. The gas is similar to ordinary air, sometimes mixed with gas generated from decaying organic matter. The solids, the water, and the gas are termed the three phases of the soil.
To aid a rational analysis of a soil mass, the three phases are “disconnected”. Soil analysis makes use of basic definitions and relations of volume, mass, density, water content, saturation, void ratio, etc., as indicated in Fig. 1.1. The definitions are related and knowledge of a few will let the geotechnical engineer derive all the others.
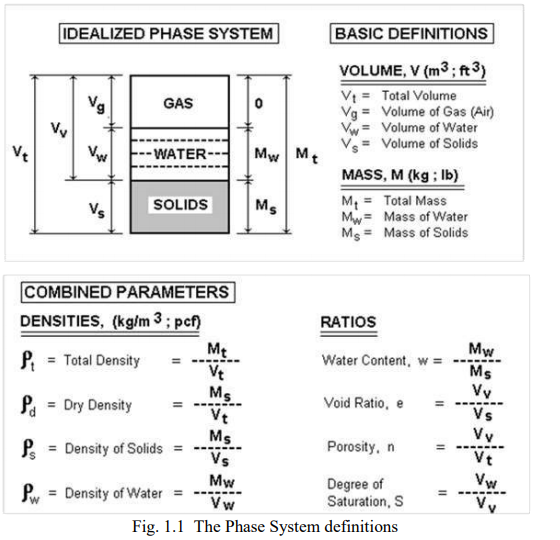
The need for phase systems calculation arises, for example, when the engineer wants to establish the effective stress profile at a site and does not know the total density of the soil, only the water content. Or, when determining the dry density and degree of saturation from the initial water content and total density in a Proctor test. Or, when calculating the final void ratio from the measured final water content in an oedometer test. While the water content is usually a measured quantity and, as such, a reliable number, many of the other parameters reported by a laboratory are based on an assumed value of solid density, usually taken as 2,670 kg/m3 plus the assumption that the tested sample is saturated. The latter assumption is often very wrong and the error can result in significantly incorrect soil parameters.
Starting from the definitions shown in Fig. 1.1, a series of useful formulae can be derived, as follows:
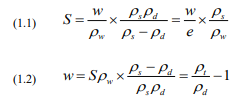
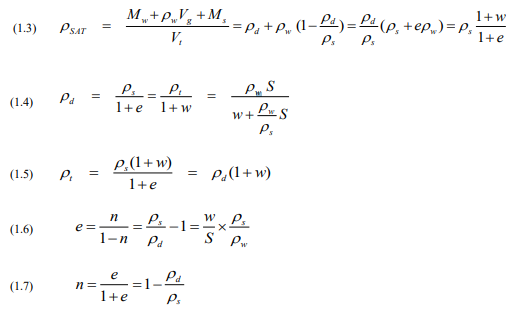
When performing phase calculations, the engineer normally knows or assumes the value of the density of the soil solids, ρs. Sometimes, the soil can be assumed to be fully saturated (however, presence of gas in fine-grained soils may often result in their not being fully saturated even well below the groundwater table; organic soils are rarely saturated and fills are almost never saturated). Knowing the density of the solids and one more parameter, such as the water content, all other relations can be calculated using the above formulae (they can also be found in many elementary textbooks, or easily be derived from the basic definitions and relations). I have included a few of the equations in an Excel “365 Cribsheet”, which can be downloaded from my web site: www.Fellenius.net.
The density of water is usually 1,000 kg/m3 . However, temperature and, especially, salt content can change this value by more than a few percentage points. For example, places in Syracuse, NY, have groundwater that has a salt content of up to 16 % by weight. Such large salt content cannot be disregarded when determining distribution of pore pressure and effective stress.
While most silica-based clays can be assumed to made up of particles with a solid density of 2,670 kg/m3 (165 pcf), the solid density of other clay types may be quite different. For example, calcareous clays can have a solid density of 2,800 kg/m3 (175 pcf). However, at the same time, calcareous soils, in particular coral sands, can have such a large portion of voids that the bulk density is quite low compared to that of silica soils. Indeed, mineral composed of different materials can have a very different mechanical response to load. For example, just a few percent of mica in a sand will make the sand weaker and more compressible, all other aspects equal (Gilboy 1928).
Organic materials usually have a dry density that is much smaller than inorganic material. Therefore, when soils contain organics, their in-place average solid density is usually smaller than for inorganic materials. Moreover, if the organic content is 3 % (of dry weight) or larger, the soil should be called “slightly organic” and at 5 % organic content, the soil should be called “organic” (as adjective). Organic soils will have smaller shear strength and larger compressibility as opposed to inorganic soils. For example, an organic clay will exhibit much increased secondary compression.
Soil grains are composed of minerals and the solid density varies between different minerals. Table 1.1 below lists some values of solid density for minerals that are common in rocks and, therefore, common in soils. The need for listing the density parameters with units could have been avoided by giving the densities in relation to the density of water, which is called “relative density”. The term relative density, as used in modern international terminology, was termed “specific gravity” in old terminology, now abandoned. However, presenting the density parameter with units, as opposed to relative to the density of water, avoids the conflict of which of the two mentioned terms to use; either the correct term, which many, but not all, would misunderstand, or the incorrect term, which all understand, but the use of which would suggest ignorance of current terminology convention. (Shifting to a home-made term, such as “specific density”, which sometimes pops up in the literature, does not make the ignorance smaller)
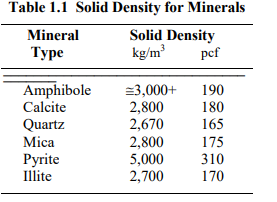
The term “relative density” is also used when describing a state of “compactness” or “compactness condition” termed “relative density”, “Dr”, which can range from very loose, loose, compact, dense, through very dense state. The relative density is not expressed in mass/volume, but is correlated to the N-index of the Standard Penetration test, SPT.
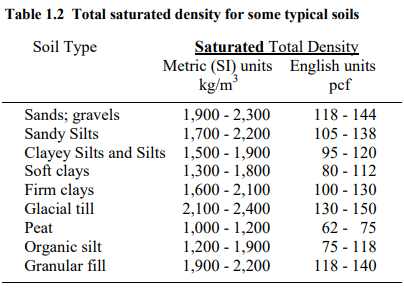
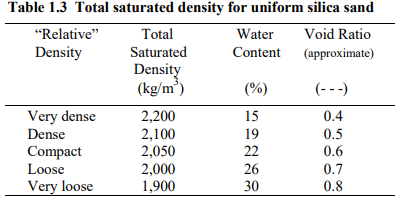
Depending on the soil void ratio and degree of saturation, the total density of soils can vary within wide boundaries. Tables 1.2 and 1.3 list some representative values.
A frequently applied expression is the “density index”, ID. The definition of the density index, ID, is based on the assumption that the void ratio of the soil can be reliably determined for standardized procedures to create “maximum” and “minimum” density of a natural soil [ID = (emax – e)/(emax – emin)]. Over the years, the density index has been used as a parameter to describe geotechnical parameters of sand deposits and correlations have been developed to estimate the angle of internal friction, liquefaction potential, and soil modulus. However, as has been shown by many, e.g., Tavenas and LaRochelle (1972), the density index is a highly imprecise and non-reproducible parameter as explained below.
A void ratio value determined on a soil sample, usually coarse-grained, is usually provided with twodecimal precision. However, the void ratio value is rarely more precise than by about 0.05±. For loose to compact sand, the in-situ void ratio typically ranges from about 0.40 through 0.60, depending on grain size gradation. Therefore, for a given sample, say, with an in-situ void ratio of 0.40, where typically, the maximum and minimum void ratios lie between 0.30 and 0.70, the ID is 75 %. However, considering that the error, very likely, would be 0.05 up or down for each of the three values, the error in a particular ID could be almost 20 %. (A 0.05 change in void ratio corresponds to a less than 2 % change in water content for a sand with e = 0.40, assuming that the degree of saturation, S, is 100 %, which is difficult to ensure for a sand sample). Tavenas and LaRochelle (1972) presented an extensive and detailed study of the Density Index and indicated that the average error is 18 % and concluded that the index “cannot be used as a base parameter of any calculation”. Indeed, any formula or numerical expression applying the ID should be considered suspect and only applied with great caution, if at all.


