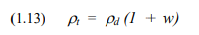As mentioned, effective stress is the total stress minus the pore pressure (the water pressure in the voids). Total stress at a certain depth below a level ground surface is the easiest of all values to determine as it is the summation of the total unit weight (total density times gravity constant) and depth. Where the pore pressure is hydrostatically distributed below the groundwater table, which is defined as the uppermost level of zero pore pressure (equal to atmospheric pressure), the pore pressure at a certain depth is equal to the density of water times the distance from that depth up to the groundwater table. (Notice, the soil can be partially saturated also above the groundwater table. Then, because of capillary action, pore pressures in the partially saturated zone above the groundwater table may be negative. In routine calculations, pore pressures are usually assumed to be zero in the zone above the groundwater table).
Notice, however, the pore pressure distribution is not always hydrostatic, far from always, actually. Hydrostatic pore water pressure has a vertical pressure gradient that is equal to unity (no vertical flow). However, the pore pressure at a site may have a downward gradient from a perched groundwater table, or an upward gradient from an aquifer down below (an aquifer is a soil layer containing free-flowing water, or a layer sandwiched between soil layers that are less “free-flowing”, i.e., less pervious). Moreover, in areas below or close to the seashore and in areas close to bedrock containing salt (NaCl), the pore water may include dissolved salt and its density may be correspondingly larger than 1,000 kg/m3 .
Frequently, the common method of determining the effective stress, Ds‘, contributed by a specific soil layer is to multiply the buoyant unit weight, g‘, of the soil with the layer thickness, Dh, as indicated in Eq. 1.8a.

The buoyant unit weight, g‘, is often thought to be equal to the total unit weight (gt) of the soil minus the unit weight of water (gw) which presupposes that there is no vertical gradient of water flow in the soil, i = 0, defined below. However, this is only a special case. Because most sites display either an upward flow (maybe even artesian; the head is greater than the depth) or a downward flow, calculations of effective stress must consider the effect of the gradient—the buoyant unit weight is a function of the gradient in the soil as follows (Eq. 1.8c).

A vertical flow is a non-hydrostatic condition. If the flow is upward, the gradient is negative; if downward it is termed positive. The flow can be minimal, that is, no obvious velocity. For artesian conditions, which is a non-hydrostatic condition, the gradient is larger than unity and the buoyant weight is smaller than for the hydrostatic condition. Then, the effective stress is smaller too and, therefore, the soil strength is reduced. For example, a “quick sand” condition occurs when the upward gradient is so large that the effective stress (and buoyant unit weight, g’), approaches zero. Note that “quick sand” is not a particularly “quick” type of sand, but a soil, usually a silty fine sand, subjected to an upward pore pressure gradient.
The gradient in a non-hydrostatic condition is often awkward to determine. However, the difficulty can be avoided, because the effective stress is most easily found by calculating the total stress and the pore water pressure separately. The effective stress is then obtained by simple subtraction of the latter from the former.
Note, the difference in terminology¾effective stress and pore pressure¾which reflects the fundamental difference between forces in soil as opposed to in water. Stress is directional, that is, stress changes depend on the orientation of the plane of action in the soil. In contrast, pressure is omni-directional, that is, independent of the orientation; equal in all directions. Don’t use the term “soil pressure”, it is a misnomer. The soil stresses, total and effective, and the water pressures are determined, as follows:
The total vertical stress (symbol sz) at a point in the soil profile (also called “total overburden stress”) is calculated as the stress exerted by a soil column determined by multiplying the soil total (or bulk) unit weight with the height of the column (or the sum of separate weights when the soil profile is made up of a series of separate soil layers having different unit weights). The symbol for the total unit weight is gt (the subscript “t” stands for “total”).
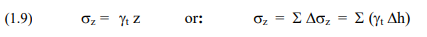
Similarly, the pore pressure (symbol u), as measured in a stand-pipe, is equal to the unit weight of water, gw, times the height of the water column, h, in the stand-pipe. (If the pore pressure is measured directly, the head of water (height of the water column) is equal to the pressure divided by the unit weight of the water, gw).
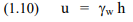
The height of the column of water (the head) representing the water pressure is usually not the distance to the ground surface nor, even, to the groundwater table. For this reason, the height is usually referred to as the “phreatic height” or the “piezometric height” to separate it from the depth below the groundwater table or depth below the ground surface.
The pore pressure distribution is determined by applying the fact that (in stationary situations) the pore pressure distribution can be assumed linear in each individual, or separate, soil layer, and, in pervious soil layers “sandwiched” between less pervious layers, the pore pressure is hydrostatic (that is, the vertical gradient within the sandwiched layer is unity. Note, if the pore pressure distribution within a specific soil layer is not linear, then, the soil layer is undergoing consolidation, which is not a stationary condition).
The effective overburden stress (symbol s¢z), also called “effective vertical stress”, is then obtained as the difference between total stress and pore pressure.
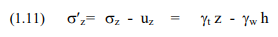
Usually, the geotechnical engineer provides a unit density, r, instead of the unit weight, g. The unit density is mass per volume and unit weight is force per volume. Because in the customary English system of units, both types of units are given as lb/volume, the difference is not clear (that one is pound-mass and the other is pound-force is not normally indicated, though pound-force is the most common variant). In the SI-system, unit density is given in kg/m3 and unit weight is given in N/m3 . Unit weight is unit density times the gravitational constant, g. (For most foundation engineering purposes, the gravitational constant can be taken to be 10 m/s2 rather than the overly exact value of 9.81 m/s2 ; besides, the second decimal varies across the Earth). Beware of asinine terms such as “weight density”.
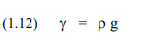
Many soil reports do not indicate the bulk or total soil density, rt , and provide only the water content, w, and the dry density, rd. Knowing the dry density, the total density of a saturated soil can be calculated as: