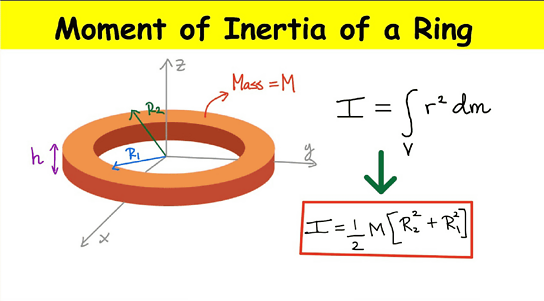
There are two theorems of moment of inertia:

(1) Perpendicular axis theorem, and

(2) Parallel axis theorem.

These are explained and proved below.

Perpendicular Axis Theorem

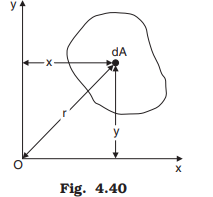
The moment of inertia of an area about an axis perpendicular to its plane (polar moment of inertia) at any point O is equal to the sum of moments of inertia about any two mutually perpendicular axis through the same point O and lying in the plane of the area.

Referring to Fig. 4.40, if z-z is the axis normal to the plane of paper passing through\ point O, as per this theorem,

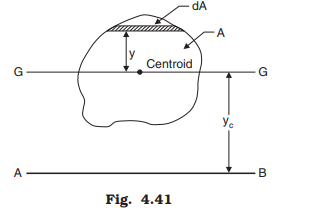
Parallel Axis Theorem

Moment of inertia about any axis in the plane of an area is equal to the sum of moment of inertia about a parallel centroidal axis and the product of area and square of the distance between the two parallel axis. Referring to Fig. 4.41 the above theorem means:

Note: The above equation cannot be applied to any two parallel axis. One of the axis (GG) must be centroidal axis only.