Introduction
All materials will undergo volume change when subjected to stress change and soils are no exception. Unlike steel or concrete and other solids, soils are made up of granular materials: grains. Moreover, the pores between the grains are usually filled with water, often a water and air (gas) mix. This fact makes the response of soil to an increase of stress more complex as opposed to other building materials. The shear strength of soil is more important for foundation design than the compressive strength, for example. The central aspect, however, is that in order for a volume change (other than the ‘elastic’ compression of the grains themselves) to take place, the space between the grains, the pores, must be able to reduce in volume. In a saturated soil, this requires that the water and/or gas first leaves the pore volume—can be squeezed out of the soil pores. The process is as follows. An increase of stress results in a small immediate, ‘initial’ or ‘elastic’, compression of the soil skeleton. If the pores contain free gas (‘bubbles’), the bubbles will compress, some of it may go into solution. This effect, too, is immediate, and the corresponding volume change (settlement) cannot be distinguished from the immediate compression. In inorganic soils, the immediate compression is small compared to the compression due to the reduction of the pore volume. However, reduction of pore volume cannot take place without the water in the pores simultaneously leaving the pores. The driving force in the latter process is the increase of pore pressure, which at first is about equal to the average of the imposed stress increase. As the water leaves the soil, the pressure reduces, “dissipates”, until, finally, all the imposed stress is carried as contact stress between the grains. The process is called “consolidation” .
The consolidation time is governed by how easy or difficult is for the water to flow through the soil along with the drainage path, the latter is the length the water has to flow to leave the zone of increased stress. The measure of the “difficulty” of the water to flow is the soil hydraulic conductivity (“permeability”) and the time is more or less a linear function of the “permeability” (related to the “coefficient of consolidation”), but it is an exponential function (square) of the drainage path. Therefore, if the drainage path can be shortened, the time for the consolidation settlement, which is the largest part of the three components of the settlement, can be shortened, “accelerated”, substantially. This is achieved by inserting drains into the soil, providing the water with the easy means of travel—”escape”—from the zone of stress increase. The spacing between the drains controls the length of the drainage path. For example, drains installed at a spacing that is a tenth of the thickness of a soil layer that is drained on both sides could, theoretically, shorten the consolidation time to a percentage point or two of the case without drains. An additional benefit is that because the water flows horizontally toward the drains (radially, rather), the flow makes use of the horizontal hydraulic conductivity of the soil, which normally is much larger than that in the vertical direction.
The potential benefit of using vertical drains became obvious very soon after Terzaghi in 1926 published his theory of consolidation. Thus, vertical drains have been used in engineering practice for almost 100 years. At first, vertical drains were made of columns of free-draining sand (sand drains) installed by various means (Barron 1947). In about 1945, premanufactured bandshaped drains, termed “wick drains”, were invented (Kjellman 1947) and, since about 1970, the technical and economic advantages of the wick drain have all but excluded the use of sand drains. Holtz et al. (1991) have presented a comprehensive account of the history of vertical drains. Lately, the preferred name is “Premanufactured Vertical Drains”, PVD. However, I have retained the “wick drain” term in this chapter.
Conventional Approach to Pore Pressure Dissipation and Consolidation of a Drain Project
The basic principles of the behavior of consolidation in the presence of vertical drains is illustrated in Fig. 4.1. The dissipation of the excess pore pressures in the soil body is governed by the water flowing horizontally toward the drain and then up to the groundwater table. (Vertical flow toward draining layers above and below the soil body is usually disregarded). The pore water pressure distribution inside the drain is assumed to be hydrostatic at all times.
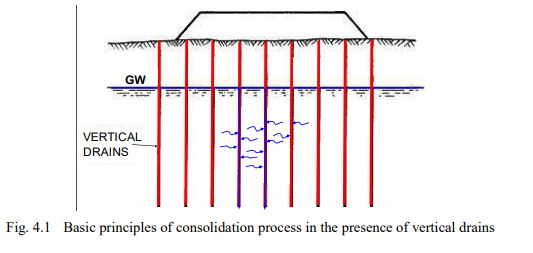
For the analysis of acceleration of pore pressure dissipation in fine-grained soils (consolidation) for a vertical drain project and subsequent settlement, Barron (1948) and Kjellman (1948) developed a theory based on radial flow toward a circular drain in the center of a cylinder of homogeneous soil with an impervious outer boundary surface (Hansbo 1960; 1979; 1981; 1994). Vertical flow (drainage) was assumed not to occur in the soil. The theory is summarized in the Kjellman-Barron formula, Eq. 4.1. The Kjellman-Barron formula is based on the assumption of presence of horizontal (radial) flow only and a homogeneous soil.

Fig. 4.2 shows a simplified sketch of the principle for consolidation of a soil layer. Fig. 4.2A shows a soil layer sandwiched between free-draining boundaries: the ground surface and a free-draining soil layer below the consolidating layer. The parabolic shape curve indicates the pore pressure distribution at a particular time. The time required for a certain degree of consolidation (in addition to the soil parameters of the case) is primarily a function of the longest drainage path, that is, half the thickness of the clay layer and assuming vertical flow.
Fig. 4.2B shows the corresponding picture where vertical drains have been installed. Here, the consolidation time is primarily a function of the spacing of the drains and horizontal flow. Note that the pore pressure in the drain is essentially hydrostatic. That is, the flow through the drain to the boundaries (ground surface and drain bottom) is a low-gradient flow. Indeed, the theoretical analysis assumes no gradient inside the drain. Therefore, testing the flow characteristics (conductivity; “ease of flow”) of wick drains should be at very low gradients. Test under a gradient of unity is common, but it could show unrealistic drain response

Relations for average degree of consolidation combining horizontal and vertical flows have been developed for vertical drains. However, the contribution of vertical drainage to the rate of consolidation is very small as opposed to the contribution by the horizontal drainage—the drainage toward the drains. In a typical case, vertical drainage alone could require 20 years, while installing drains to facilitate horizontal drainage could shorten the time to 3 months. Obviously, the contribution of the vertical drainage is usually minimal.
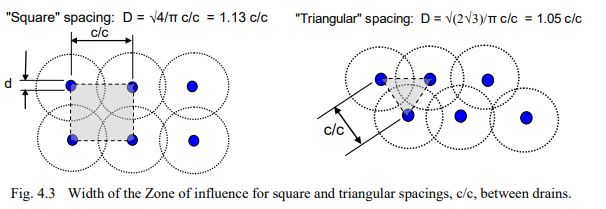
The zone of influence of a drain is defined as the diameter of a cylinder having the same cross section area as the area influenced by the drain. That is, if in a given large area of Size A there are n drains placed at some equal spacing and in some grid pattern, each drain influences the area A/n. Thus, for drains with a center-to-center spacing, c/c, in a square or triangular pattern, the zone of influence, D, is 1.13 c/c or 1.05 c/c, respectively, as illustrated in Fig. 4.3. In the case of sand drains, the equivalent diameter, d, is often taken as equal to the nominal diameter of the sand drain.
In the case of wick drains (Section 4.5), no agreement exists on what to use as the equivalent diameter of the drain. One approach used is simply to equalize the outside surface area of the wick drain with a circular sand drain of the same surface. However, this approach does not recognize the difference between the usually open surface of the premanufactured drain and the rather closed surface of the sand drain, nor the differences between various makes of wick drains. Strictly speaking, the equivalent diameter of a wick drain should be termed “the equivalent cylinder diameter” to separate it from ‘the equivalent sand drain diameter’. Fellenius (1977) suggested that the equivalent cylinder diameter of a sand drain is the nominal diameter of the sand drain multiplied by the porosity of the sand in the drain. The porosity of loose, free-draining sand is normally about 0.4 to 0.5. Thus, the equivalent cylinder diameter of a sand drain is about half of the nominal diameter.
However, the question of what value of equivalent diameter to use is not of importance in practice because the consolidation time is not very sensitive to the variations of the value of the equivalent cylinder diameter. (In contrast, the consolidation time is very sensitive to the spacing of the drains). For wick drains of, commonly, 100-mm width, values proposed as the equivalent cylinder diameter have ranged between 30 mm and 80 mm, and full-scale studies have indicated that the performance of such drains have equaled the performance of sand drains of 200 mm to 300 mm in nominal diameter (Hansbo 1960; 1979; 1981; 1994).
The average degree of consolidation at a certain time, U , is defined as the ratio between the average increase of effective stress, Ds’, in the soil over the applied stress causing the consolidation process, i.e., Ds’/q. In practice, average degree of consolidation is determined from measurements of either pore pressure increase or settlement and defined as 1 minus the ratio between the average pore pressure increase in the soil over the total pore-pressure increase resulting from the applied stress, U =1 – u/u0, or, U =DS/Sf , the amount of settlement obtained over the final amount of settlement at completed consolidation. Because pore pressures can be determined at the start of a project, whereas the value of the final settlement is not obtained until after the project is completed, the degree of consolidation is usually based on pore pressure measurements. However, pore pressures and pore-pressure dissipation vary with the distance to the draining layer and, in particular, with the distance to the drains. Seasonal variation is also a factor. Therefore, and in particular because pore-pressure measurements are usually made in only a few points, pore pressure values are very imprecise references to the average degree of consolidation.
The rate of consolidation may differ at different depths and locations due not least to variations of layer thickness. Therefore, also the average degree of consolidation based on settlement observations is also a rather ambiguous value, unless related to measurements of the compression of each specific layer (difference between settlement at top and bottom of the layer) and as the average of several such layers.
In a homogeneous soil layer, the horizontal coefficient of consolidation, ch, is usually several times larger than the vertical coefficient, cv. Moreover, dissipation time calculated according to the Kjellman-Barron formula (Eq. 4.1), is inversely proportional to the ch-value. Note, however, that the drain installation will disturb the soil and break down the horizontal pathways nearest the drain (create a “smear zone”) and, therefore, the benefit of the undisturbed horizontal coefficient may not be available.
For sand drains, in particular displacement-type sand drains, a ch-value greater than the cv -value can rarely be mobilized. For a detailed theoretical calculation, to consider the effect of a smear zone would seem necessary. However, in practice, other practical aspects (See Section 4.3) are far more influential for the process of accelerating settlement and theoretical refinements are rarely justified (see also Section 4.6.7) and Considering smear zone effect could distract the attention from the far more important aspects of choosing representative parameters and assessing the site conditions correctly.
The coefficient of consolidation, cv , varies widely in natural soils (see Section 3.8). In normally consolidated clays, it usually ranges from 1×10-8 m 2 /s to 30×10-8 m 2 /s (3 to 100 m2 /year). In silty clays and clayey silts, it can range from 5×10-8 m 2 /s to 50×10-8 m 2 /s (16 to 160 m2 /year).
The coefficient of consolidation, cv , is normally determined from laboratory testing of undisturbed soil samples or, preferably, in-situ by determining the pore-pressure dissipation time in a piezocone (CPTU; see Chapter 2). The actual ch-coefficient to use requires considerable judgment in its selection, and it can, at best, not be determined more closely than within a relative range of three to five times. This means that engineering design of a project requires supporting data for selection of the ch- coefficient in order to avoid the necessity of employing an excessively conservative approach.
The duration of the primary consolidation without the presence of vertical drains can take many years. When drains have been installed, the duration is typically shortened to a few months. Also a vertical drain project will include estimating the magnitude and rate of the secondary compression (Chapter 3, Section 3.9), which involves calculations with input of coefficient of secondary compression, Cα, and duration of the primary consolidation tCONS. First, the Cα is considered to be a soil parameter that is independent of whether the consolidation is achieved by vertical or horizontal drainage. Then, using the, typically, 50 to 100 times shorter time for tCONS for horizontal drainage (wick drains case) as opposed to that for vertical drainage will result in that the calculated settlement due to secondary compression will come out as an order of magnitude larger for a project where the consolidation process is having accelerated by means of vertical drains, as opposed to the number for where no vertical drains are used. Secondary compression is not governed by the direction of water flow nor can it reasonably be a function of the length of the drainage path. Therefore, the discrepancy is not true. It is the result of the fact mentioned in Section 3.9 that the secondary compression concept is an empirical approach to fit observations to some reasonable way of calculating and predicting the process. To resolve the discrepancy, when estimating the magnitude of secondary compression developing after the end of consolidation for a vertical drain project, the duration required for the consolidation had there been no drains should be estimated and used in calculating the settlement due to secondary compression.

